第四节 绝对值　

典型例题

　　例1 求下列各数的绝对值：

　　(1)-38；　(2)0.15；

　　(3)a(a＜0)； (4)3b(b＞0)；

　　(5)a-2(a＜2)； (6)a-b．

　　分析：欲求一个数的绝对值，关键是确定绝对值符号内的这个数是正数还是负数，然后根据绝对值的代数定义去掉绝对值符号，(6)题没有给出a与b的大小关系，所以要进行分类讨论．

　　解：(1)|-38|＝38；(2)|+0.15|＝0.15；

　　(3)∵a＜0，∴|a|＝-a；

　　(4)∵b＞0，∴3b＞0，|3b|＝3b；

　　(5)∵a＜2，∴a-2＜0，|a-2|＝-(a-2)＝2-a；

　　

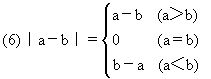
　　点拨：分类讨论是数学中的重要思想方法之一，当绝对值符号内的数(用含字母的式子表示时)无法判断其正、负时，要化去绝对值符号，一般都要进行分类讨论．

　　例2 判断下列各式是否正确(正确入“T”，错误入“F”)：

　　(1)|-a|＝|a|；　( )

　　(2)-|a|＝|-a|；　( )

　　

　　(4)若|a|＝|b|，则a＝b；  ( )

　　(5)若a＝b，则|a|＝|b|；  ( )

　　(6)若|a|＞|b|，则a＞b；( )

　　(7)若a＞b，则|a|＞|b|；( )

　　(8)若a＞b，则|b-a|＝a-b．( )

　　分析：判断上述各小题正确与否的依据是绝对值的定义，所以思维应集中到用绝对值的定义来判断每一个结论的正确性．判数(或证明)一个结论是错误的，只要能举出反例即可．如第(2)小题中取a＝1，则-|a|＝-|1|＝-1，而|-a|＝|-1|＝1，所以-|a|≠|-a|．同理，在第(6)小题中取a＝-1，b＝0，在第(4)、(7)小题中取a＝5，b＝-5等，都可以充分说明结论是错误的．要证明一个结论正确，须写出证明过程．如第(3)小题是正确的．证明步骤如下：

　　

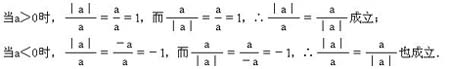
　　化去绝对值符号即可．对于证明第(1)、(5)、(8)小题要注意字母取零的情况．

　　解：其中第(2)、(4)、(6)、(7)小题不正确，(1)、(3)、(5)、(8)小题是正确的．

　　点拨：判断一个结论是正确的与证明它是正确的是相同的思维过程，只是在证明时需要写明道理和依据，步骤都要较为严格、规范．而判断一个结论是错误的，可依据概念、性质等知识，用推理的方法来否定这个结论，也可以用举反例的方法，后者有时更为简便．

　　例3判断对错．(对的入“T”，错的入“F”)

　　(1)如果一个数的相反数是它本身，那么这个数是0． (   )

　　(2)如果一个数的倒数是它本身，那么这个数是1和0． (   )

　　(3)如果一个数的绝对值是它本身，那么这个数是0或1． (   )

　　(4)如果说“一个数的绝对值是负数”，那么这句话是错的． (   )

　　(5)如果一个数的绝对值是它的相反数，那么这个数是负数． (   )

　　解：(1)T．

　　(2)F．-1的倒数也是它本身，0没有倒数．

　　(3)F．正数的绝对值都等于它本身，所以绝对值是它本身的数是正数和0．

　　(4)T．任何一个数的绝对值都是正数或0，不可能是负数，所以这句话是错的．

　　(5)F．0的绝对值是0，也可以认为是0的相反数，所以少了一个数0．

　　点拨：解判断题时应注意两点：

　　(1)必须“紧扣”概念进行判断；

　　(2)要注意检查特殊数，如0，1，-1等是否符合题意．

返回页首