第四节 动能 动能定理

典型例题

例题1：

　　水平恒力F作用在物体上，物体在光滑水平面上沿力的方向移动s距离，恒力做功为 ，物体获得的动能为 ．若该恒力作用在同一物体上，物体在粗糙水平面上移动相同距离，恒力做功为 ，物体获得的动能为 则（  ）

　　A． 　　　B．

　　C． 　　　D．

　　分析与解  根据功的定义式 ，可得 。

　　解法1  由牛顿定律知 ，在光滑平面上， ，在粗糙平面上， 所以 ，所以 ，则 。

　　解法2  由动能定理， ，在光滑平面上，只有F做功，粗糙平面上除F外还有阻力f做功， ，所以 。

　　解法3  由功能关系，在光滑水平面上，F做的功即为物体动能的增加量， ；在粗糙水平面上，F做的功 与 相同．但这个功不仅使物体动能增加，而且还通过物体克服摩擦力做功使物体的内能增加，即 ，所以 。

　　综上所述，本题应选C。

例题2：一物体从斜面底端以初动能E滑向斜面，返回到底端的速度大小为v，克服摩擦力做功为 ，若物块以初动能2E滑向斜面，则（   ）

　　A．返回斜面底端时的动能为E

　　B．返回斜面底端时的动能为

　　C．返回斜面底端时的速度大小为2v

　　D．返回斜面底端时的速度大小为

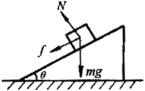
　　分析与解  物体m在斜面上升时，受力分析如图所示．沿斜面下滑时，滑动摩擦力f方向沿斜面向上．

解法1  应用运动学知识．

　　以初动能E上滑时， ，上滑的最大位移为s， ，则有

　　　　　　　　①

　　返回时    　　　②

　　　　　　　　③

　　以2E初动能上滑，上滑的最大位移为 则有

　　　　　　　　④

　　返回时     　　　⑤

　　　　　　　　　⑥

　　由①、④两式得 。

　　由②、⑤两式得 ，所以

　　由③、⑥两式得 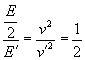，所以 。

解法2  应用动能定理，

　　设物块以初动能E上滑时，最大位移为s．

　　　　　　①

　　返回到出发点           　　　②

　　返回时动能             　　　　　　③

　　设物块以初动能2E上滑时，最大位移为 。

　　上滑过程                 　　④

　　返回出发点               　　　　⑤

　　返回时速度为              　　　⑥

　　由①、④两式得 。

　　由②、⑤两式得 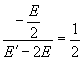，所以 。

　　由③、⑥两式得 ，所以 。

解法3  应用功能关系。

　　以初动能E上滑时             

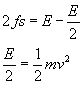
　　以初动能2E上滑时            

　　　

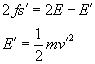
　　解上述六个式子，得 ， 。

　　综上所述，选项A、D正确。

例题3：如以竖直初速度 抛出一个质量为m的小球，当小球返回出发点时的速度大小为 ，求小球在运动过程中受的平均阻力f和小球能上升的最大高度。设小球上升的最大高度为h，上升过程中小球受重力和空气阻力（方向向下），这二个力都对物体做负功，小球初动能为 ，末动能为零，由动能定理有

　　　　　　①

　　下落过程小球受重力和空气阻力（方向向上），重力对小球做正功，空气阻力为小球做负功，小球初动能为零，末动能为 ，根据动能定理

　　　　　　②

　　将①、②式相比得

　　

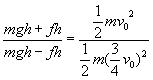
　　解得   

　　　将 代入①式得    。

　　也可以对小球上升和下落的全过程应用动能定理，全过程，重力做功为零（ ），空气阻力始终做负功，初动能 ，末动能 ，有

　　　　　③

　　由①③联立解得f、h。

　　用动能定理还可以解决一些运动过程和受力情况均较为复杂的力学问题，在例题中再作讲解。

例题：如图4所示，用细绳连接的A、B两物体质量相等，A位于倾角为30°的斜面上，细绳跨过定滑轮后使A、B均保持静止，然后释放，设A与斜面间的滑动摩擦力为A受重力的0.3倍，不计滑轮质量及摩擦，求B下降1米时的速度．

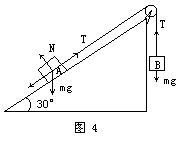
　　如果自由选择研究对象，那么可能有人选择A、B为研究对象，而有人则将A、B看成一个整体来分析，解题过程：

　　

　　　　　　　

　　三式联立解得：v＝1.4米/秒

　　解法二：将A、B看成一整体．(因二者速度、加速度大小均一样)，此时拉力T为内力，求外力做功时不计，则动能定理写为：

　　

　　f＝0.3mg

　　二式联立解得：v＝1.4米/秒

　　可见，结论是一致的，而方法二中受力体的选择使解题过程简化，因而在使用动能定理时要适当选取研究对象．

返回页首