 设为首页
设为首页
 加入收藏
加入收藏
教学设计方案一
9.8棱锥 第一课时
教学目标:
1.理解棱锥的概念、分类.
2.掌握棱锥中平行于底面的截面与原棱锥底面的关系的定理.
3.记住锥体的体积公式.
教具准备:投影胶片、三角板.
教学过程:
[设置情境]
(投影出实际生活中常见的棱锥的例子)
问:那么棱锥应该怎么去定义呢?
[探索研究]
1.介绍概念
棱锥的定义、侧面、棱锥的高、侧棱、顶点.(图1)
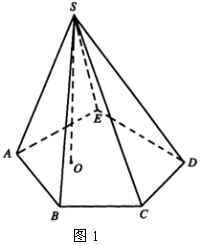
2.分类
从底面多边形的边来分可分为:三棱锥、四棱锥…(图2)
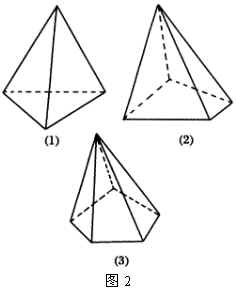
3.棱锥的性质
定理 如果棱锥被平行于底面的平面所截,那么截面和底面相似,并且它们面积的比等于截得的棱锥的高与已知棱锥的高的平方比.
证明:(见课本P48)
4.棱锥的体积
![]() (其中
(其中![]() 是锥体的底面积,
是锥体的底面积,![]() 是锥体的高.)
是锥体的高.)
5.例题分析
例1 若两个平行于底面的截面恰好三等分棱锥的体积,求此棱锥的高被截面分得的三条线段的长之比.
解:由棱锥的性质可知,用平行于底面的平面截棱锥,它们的面积比等于对应高的平方比.容易推出它们的体积比为对应高的立方比.
设以截面为底的棱锥的高与原棱锥的高分别为![]() 、
、![]() 、
、![]() (
(![]() ),则
),则![]() ,又
,又![]() ,故
,故![]() ,
,
∴![]() .
.
于是![]() .
.
例2 已知三棱锥的顶点在底面内的射影为底面三角形的垂心,求证:底面内任一顶点在其相对侧面内的射影也是此侧面三角形的垂心.
证明:如图3,在三棱锥![]() 中,
中,![]() 在底面内的射影
在底面内的射影![]() 为△
为△![]() 的垂心,
的垂心,![]() 、
、![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() .
.
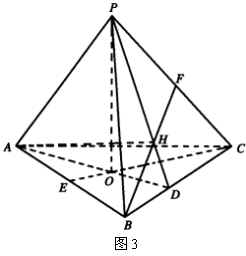 作
作![]() 面
面![]() 于点
于点![]() ,连
,连![]() 、
、![]()
∵![]() 为△
为△![]() 的垂心
的垂心
∴![]()
由三垂线定理得![]() ,再由三垂线定理知
,再由三垂线定理知![]()
同理∵![]()
∴![]()
∴![]() (三垂线定理)
(三垂线定理)
∴![]() 为△
为△![]() 的垂心
的垂心
同理可证![]() 、
、![]() 在△
在△![]() 、△
、△![]() 上的射影也分别是它们的垂心.
上的射影也分别是它们的垂心.
例3 如图4,四棱锥的高为![]() ,底面为菱形,侧面
,底面为菱形,侧面![]() 和侧面
和侧面![]() 所成的二面角为
所成的二面角为![]() ,且都垂直于底面,另两个侧面与底面所成的角都等于
,且都垂直于底面,另两个侧面与底面所成的角都等于![]() ,求此棱锥的全面积.
,求此棱锥的全面积.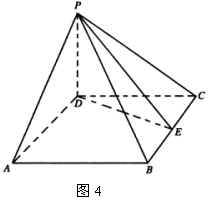
解:因侧面![]() 底面
底面![]() ,侧面
,侧面![]() 底面
底面![]() ,故
,故![]() 底面
底面![]() .
.![]() 为二面角
为二面角![]() 的平面角,即
的平面角,即![]() .
.
因四边形![]() 是菱形,故△
是菱形,故△![]() 为正三角形.取
为正三角形.取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]() ,则
,则![]() ,又由三垂线定理可知
,又由三垂线定理可知![]() ,故
,故![]() 是侧面
是侧面![]() 与底面
与底面![]() 所成的二面角的平面角,
所成的二面角的平面角,![]() .
.
在![]() △
△![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且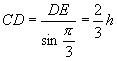 ,
,
∴![]() +
+ ![]()
![]()
![]()
![]() .
.
教师点评:本例是一个典型的题型,既可复习棱锥的概念又可复习线、面之间的平行、垂直关系.
[演练反馈]
1.正方体![]() 中,以
中,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的三棱锥与正方体的体积之比为(
)
为顶点的三棱锥与正方体的体积之比为(
)
A.![]() B.1:3 C.3:1 D.
B.1:3 C.3:1 D.![]()
2.三棱锥![]() 各侧面与底面所成的二面角都是
各侧面与底面所成的二面角都是![]() ,底角三角形的三边长分别为3、4、5,求此棱锥的则面积.
,底角三角形的三边长分别为3、4、5,求此棱锥的则面积.
3.过棱锥高的两个三等分点作平行于底面的截面,设两个截面面积及底面面积分别为![]() 、
、![]() 、
、![]() ,(
,(![]() ),求
),求![]() .
.
[参考答案]
1.B 2.12 3.1:4:9
[总结提炼]
棱锥中平行于底面的截面与原棱锥底面关系的定理中的有关结论可作适当推广.如果飘棱锥被平行于底面的平面所截,那么截得小棱锥与原棱锥的对应面(底面、侧面等)之比,等于对应线段(高、侧棱等)的平方比.同样截得小棱锥与原棱锥的体积之比等于对应线段的立方比.这里要强调的是必须为两棱锥的对应的量.
布置作业:
1.课本P52习题9.8 5.
2.课本P52习题9.8 6.
3.如图1,在四棱锥![]() 中,侧面
中,侧面![]() 是正三角形,且垂直于底面,又底面
是正三角形,且垂直于底面,又底面![]() 是矩形,
是矩形,![]() 是侧棱
是侧棱![]() 的中点.
的中点.
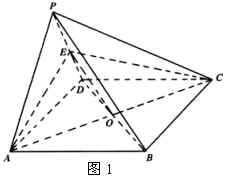 (1)求证:
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)若![]() ,且
,且![]() ,求
,求![]() .
.
[参考答案]
1.1:9 2.略.
3.(1)提示:![]() (2)提示:
(2)提示:![]() 平面
平面![]() (3)
(3)![]()
板书设计:
| 1.棱锥的概念 (1) (2) (3) |
定理 例1 例2 |
例3 练习 |
教学设计方案二
9.8 棱锥 第二课时
教学目标:
1.理解正棱锥的定义.
2.理解、掌握正棱锥的性质.
教具准备:
三角板、投影胶片.
教学过程:
[设置情境]
棱柱有正斜之分,那么棱锥是否也有正斜之分呢?如果有的话,那么什么叫正棱锥呢?正棱锥有什么性质呢?
[探索研究]
1.正棱锥
定义:如果一个棱锥的底面是正多边形,并且顶点在底面内的射影是底面中心,这样的棱锥叫做正棱锥.
2.正棱锥的性质
(1)各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等,它叫做正棱锥的斜高.
(2)棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形;棱锥的高、侧棱和侧棱在底面内的射影也组成一个直角三角形.(如图1)
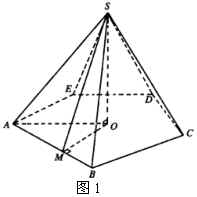
3.例题分析
例1 如图2,已知正三棱锥![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,且平面
的中点,且平面![]() 平面
平面![]() ,求正三棱锥
,求正三棱锥![]() 的侧面积与底面积之比.
的侧面积与底面积之比.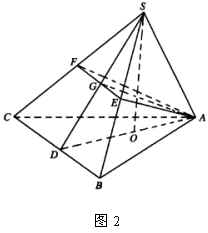
解:作正棱锥的高![]() ,连结
,连结![]() 并延长,交
并延长,交![]() 于
于![]() ,连结
,连结![]() 交
交![]() 于
于![]() ,连结
,连结![]() .
.
∵![]() 平面
平面![]() ,
,![]() 是△
是△![]() 中心,故
中心,故![]() 是
是![]() 的中点.又
的中点.又![]() 是△
是△![]() 的中位线,故
的中位线,故![]() 是
是![]() 的中点,根据对称性,
的中点,根据对称性,![]() ,
,
∴![]() .因平面
.因平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,有
,有![]() ,△
,△![]() 是等腰三角形,
是等腰三角形,![]() .
.
设正三棱锥![]() 的底面边长为
的底面边长为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .于是
.于是
 .
.
例2 如图3(1),在正四棱锥![]() 中,高
中,高![]() ,底面边长为
,底面边长为![]() ,求:
,求: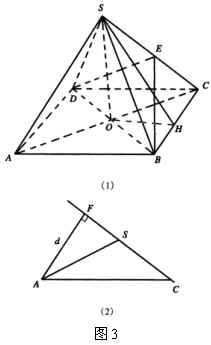
(1)侧面与底面的夹角![]() ;
;
(2)顶点![]() 到侧棱
到侧棱![]() 的距离;
的距离;
(3)相邻两侧面的夹角![]() .
.
解:(1)由![]() 底面
底面![]() 知
知![]() 为底面正方形
为底面正方形![]() 的中心,过
的中心,过![]() 作
作![]() 于
于![]() ,连结
,连结![]() .
.
由三垂线定理可知![]() ,故
,故![]() 为侧面与底面所成二面角的平面角,即
为侧面与底面所成二面角的平面角,即![]() ,在
,在![]() △
△![]() 中,
中,![]() ,故
,故![]() ,
,![]() .
.
(2)如图3(2),![]() ,
,![]() ,
,![]() .过
.过![]() 作
作![]() 的延长线于
的延长线于![]() ,由
,由![]() 知,
知,![]() ,故得
,故得![]() .即
.即![]() 到
到![]() 的距离为
的距离为![]() .
.
(3)过![]() 作
作![]() 于
于![]() ,连结
,连结![]() .由△
.由△![]() ≌△
≌△![]() ,得
,得![]() ,故
,故![]() ,
,![]() 为二面角
为二面角![]() 的平面角,
的平面角,![]() ,
,![]() .
.![]() .
.
∴![]() .
.
在△![]() 中,
中,![]()
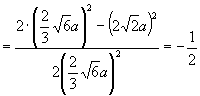 .
.
又![]()
∴![]() .
.
例3 如图4,在三棱锥中![]() 中,△
中,△![]() 是正三角形,
是正三角形,![]() ,
,![]() 为
为![]() 中点,二面角
中点,二面角![]() 为
为![]() ,
,![]() ,
,![]()
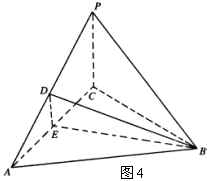
(1)求证:![]() ;
;
(2)求![]() 与底面
与底面![]() 所成的角(反正弦表示);
所成的角(反正弦表示);
(3)求三棱锥![]() 的体积.
的体积.
解:(1)取![]() 中点
中点![]() ,连结
,连结![]() 、
、![]() ,则
,则![]() .由
.由![]() ,知
,知![]() .由△
.由△![]() 为正三角形,得
为正三角形,得![]() .又
.又![]() ,所以
,所以![]() 平面
平面![]() ,
,![]() 平面
平面![]() .于是
.于是![]() .
.
(2)由![]() 平面
平面![]() ,
,![]() 底面
底面![]() ,知平面
,知平面![]() 底面
底面![]() ,
,![]() 是
是![]() 与底面
与底面![]() 所成的角.
所成的角.
由![]() ,
,![]() ,知
,知![]() 是二面角
是二面角![]() 的平面角,在△
的平面角,在△![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
故得![]() ,
,![]() .
.
由正弦定理得![]()
∴![]()
∴所求的角为![]() .
.
(3)∵![]() 平面
平面![]() ,
,![]() 底面
底面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
作![]() 到平面
到平面![]() 的垂线
的垂线![]() ,
,![]() 为垂足,
为垂足,![]() 在
在![]() 的延长线上.在
的延长线上.在![]() △
△![]() 中,
中,![]() ,
,![]() ,故
,故![]() .
.
![]()
![]() .
.
教师点评:此题更简单的解法,可以作![]() 垂直线
垂直线![]() 于点
于点![]() ,证明
,证明![]() 面
面![]() ,指出
,指出![]() 为问题(2)所求并且把
为问题(2)所求并且把![]() 放在
放在![]() △
△![]() 中去求(先证
中去求(先证![]() ,再算出世
,再算出世![]() 、
、![]() 、
、![]() ),问题(3)中
),问题(3)中![]() 到面
到面![]() 的距离为
的距离为![]() 到面
到面![]() 的距离
的距离![]() 的2倍,从而
的2倍,从而![]() .
.
[演练反馈]
1.有下列棱锥:①各侧棱都相等的棱锥.②底面是正多边形的棱锥.③顶点在底面上的射影是底面多边形外接圆圆心的棱锥.④侧面都是全等的等腰三角形的棱锥,其中为正棱锥的有( )
A.0个 B.1个 C.2个 D.3个
2.正三棱锥![]() 的底面边长为
的底面边长为![]() ,侧棱长为
,侧棱长为![]() ,经过棱
,经过棱![]() 和
和![]() 的两个中点
的两个中点![]() 、
、![]() 作一平行于
作一平行于![]() 的截面,求截面面积.
的截面,求截面面积.
3.如图1,已知正三棱锥![]() 的高
的高![]() ,斜高
,斜高![]() ,求经过
,求经过![]() 的中点且平行于底面的截面△
的中点且平行于底面的截面△![]() 的面积.
的面积.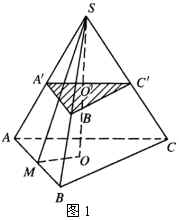
[参考答案]
1.A 2.![]()
3.解:由已知得![]()
又设底面三角形边长为![]()
则![]()
∴![]()
∴![]()
∴![]() .
.
[总结提炼]
正棱锥要有两条保证,一是底面是正多边形,二是顶点在底面上的射影是底面的中心,应用时应多加注意.
布置作业:
1.课本P53习题9.8 8.
2.课本P53习题9.8 9.
3.课本P53习题9.8 10.
[参考答案]
1.![]() 2.(1)
2.(1)![]() 倍 (2)
倍 (2)![]()
3.使截得的棱锥的高与原棱锥的高的比为![]()
板书设计:
|
1.正棱锥 2.正棱锥的性质 |
例1 例2 |
例3 |
教学设计方案三
9.8 棱锥 第三课时
教学目标:
理解正多面体的概念,了解正多面体的种类,懂得什么叫凸多面体.
教具准备:三角板.
教学过程:
[设置情境]
我们知道正多边形的边数可以是大于等于3的任意自然数,那么正多面体的面数是否也可以有任意多个呢?
[探索研究]
1.多面体的概念
多面体——若干个平面多边形围成的几何体.
多面体的面、多面体的棱、多面体的顶点如图1.
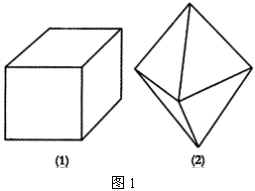
2.凸多面体的概念
把多面体的任何一个面伸展为平面,如果所有其他各面都在这个平面的同侧,这样的多面体叫做凸面体.
3.多面体的分类
一个多面体至少有四个面.多面体依照它的面数分别叫做四面体、五面体、六面体等.
4.正多面体的定义及种类
正多面体——每个面都具有相同边数的正多边形,且以每个顶点为其一端都有相同数目的棱的凸多面体.
正多面体只有五种:正四面体、正六面体、正八面体、正十二面体和正二十面体.
5.例题分析
例1 设![]() 简单多面体},
简单多面体},![]() {凸多面体},
{凸多面体},![]() {正多面体},则
{正多面体},则![]() 、
、![]() 、
、![]() 之间的关系是(
)
之间的关系是(
)
A.![]()
![]()
![]()
![]()
![]() B.
B.![]()
![]()
![]()
![]()
![]()
C.![]()
![]()
![]()
![]()
![]() D.
D.![]()
![]()
![]()
![]()
![]()
解:简单多面体包括:棱柱、棱锥、正多面体、凸多面体等,所以A,B都错误,又根据正多面体的定义,正多面体是特殊的凸多面体,所以D错误,正确的是C.
例2 两个棱长相等的正多面体,将它们的一个面重合,得到的多面体是不是正多面体?(如图2)
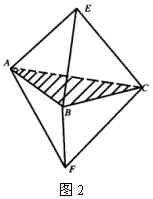
解:设将两个正四面体的一个面重合,根据正多面体的定义,每个顶点都有相同数目的棱数,而重合后的那个面上的三个顶点都有4条棱,不重合的那两个顶点各有3条棱,所以重合后得到的多面体不是正多面体.
教师点评:判断一个凸多面体是不是一个正多面体,只要根据定义看看这个多面体的每个面是否是全等的正多边形以及每个顶点是否有相同数目的棱数.
例3 求棱长为![]() 的正八面体的体积
的正八面体的体积![]() 和全面积
和全面积![]() .
.
解:如图3,易知截面![]() 是一个边长为
是一个边长为![]() 的正方形,并且它把正八面体分成两个全等的正四棱锥
的正方形,并且它把正八面体分成两个全等的正四棱锥![]() 和
和![]() .
.
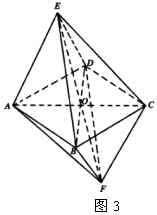
设![]() 是棱锥
是棱锥![]() 的高,
的高,
则
∴![]()
![]() .
.
例4 已知四面体各棱长是1或2,且该四面体不是正四面体,求其体积.
解:由于四面体不是正四面体,且由三角形的两边之和大于第三边,又根据题没,可知棱长是1的棱只可能有1条、2条、3条三种情况: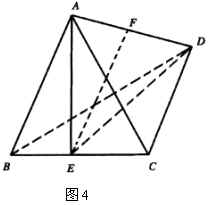
(1)如图4,若四面体![]() 中,
中,![]() 的棱长是1,其余各棱的长是2,分别取
的棱长是1,其余各棱的长是2,分别取![]() 、
、![]() 的中点
的中点![]() 、
、![]() ,连结
,连结![]() 、
、![]() 、
、![]()
因为△![]() 和△
和△![]() 均是以
均是以![]() 为底边的等腰三角形.
为底边的等腰三角形.
∴![]() ,
,![]() .又
.又![]() 面
面![]() ,
,![]() 面
面![]() ,且
,且![]()
∴![]()
![]() .
.
∴![]()
易证:![]() ,
,
因为![]() ,所以
,所以![]() .
.
在![]() △
△![]() 中,
中,
得![]()
在![]() △
△![]() 中,得
中,得![]()
∴![]()
∴![]() .
.
(2)如图5,若四面体![]() 中,
中,![]() 和
和![]() 的棱长是1,其余各棱长是2,同(1)可得
的棱长是1,其余各棱长是2,同(1)可得![]() .
.
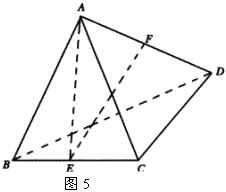
(3)如图6,若四面体![]() 中,
中,![]() 、
、![]() 、
、![]() 的棱长都是1,其余各棱长是2,作
的棱长都是1,其余各棱长是2,作![]() 面
面![]()
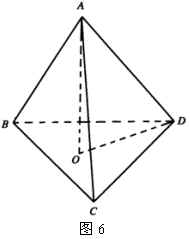
因为![]() ,则垂足
,则垂足![]() 是底面正△
是底面正△![]() 的中心,连结
的中心,连结![]() ,到
,到![]() ,在
,在![]() △
△![]() 中,
中,![]() ,又
,又![]() ,
,
所以![]() .
.
[演练反馈]
1.正方体、正多面体、凸多面体、简单多面体、多面体之间有什么关系?
2.求证:正四面体的二面角与正八面体的二面角互为补角.
3.已知一个正多面体的体积为![]() ,它的一个侧面积为
,它的一个侧面积为![]() ,则由正多面体的一点到各侧面的距离之和等于____________.
,则由正多面体的一点到各侧面的距离之和等于____________.
4.正四面体相邻两个面所成的二面角的平面角的余弦值是__________.
[参考答案]
1.{正方体} ![]() {正多面体}
{正多面体} ![]() {凸多面体}
{凸多面体} ![]() {简单多面体}
{简单多面体} ![]() {多面体}
{多面体}
2.提示:设正四面体的二面角为![]() ,正八面体的二面角为
,正八面体的二面角为![]() .
.![]() (
(![]() ),
),![]() ∴
∴![]() .
.
3.![]() 4.
4.![]()
[总结提炼]
本节课主要学习了多面体的定义、凸多面体的定义、正多面体的定义及种类,正多面体的面数已经不像正多边形边数那样有无数多种类型了,而只有4、6、8、12、20五种,要想知道为什么,等到学习了欧拉公式就明白了.
板书设计:
|
1.多面体 2.正多面体 例1 |
例2 例3 |
例4 |