 设为首页
设为首页
 加入收藏
加入收藏
教学设计示例一
9.6 两个平面垂直的判定和性质 第一课时
教学目标:
1.理解二面角的有关概念,能画出二面角.
2.会求二面角的平面角.
教具准备:投影胶片、三角板.
教学过程:
[设置情境]
看看日常生活中常见的例子:公路上的坡面与水平面,打开的门与门框所在的平面等.它们中的两个面成一定的角度.为了解决实际问题,人们需要研究两个平面所成的角.那么,怎么定义两个平面所成的角呢?
[探索研究]
1.二面角
(1)半平面
平面内的一条直线把这个平面分成两部分,其中的每一部分都叫做半平面.
(2)二面角
从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个半平面叫做二面角的面.
(3)二面角的画法:分直立式与平卧式两种.图1,记作二面角 ![]() .
.
①直立式 ②平卧式
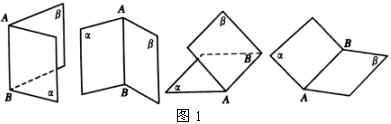
2.二面角的平面角
教师提出问题:平面几何中可以把角理解为一个旋转量,同样,一个二面角也可以看作是一个半平面以其棱为轴旋转而成的,也是一个旋转量.这说明二面角不仅有大小.而且其大小是惟一确定的.
平面与平面的位置关系,总的说来只有相交或平行两种情况.为了对相交平面的相互位置作进一步的探讨,我们有必要来研究二面角的度量问题.从而提问:二面角的大小应该怎么度量?
让学生主动动手操作并与同学讨论交流,尝试找到度量二面角大小的方法.
现给出二面角的平面角的定义:
以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.
如图2,二面角 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
. ![]() 是二面角
是二面角 ![]() 的平面角.
的平面角.
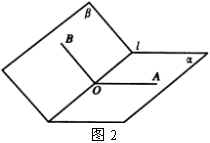
二面角的平面角的范围是 ![]() ,当两个半平面重合时,平面角为
,当两个半平面重合时,平面角为 ![]() ;当两个半平面合成一个平面时,平面角为
;当两个半平面合成一个平面时,平面角为 ![]() .求解二面角问题的关键是确定平面角的位置,需抓住“二面角的平面角”的三个要素:(1)确定二面角的棱上一点;(2)经过这点分别在两个面内引射线;(3)所引的射线都垂直于棱.
.求解二面角问题的关键是确定平面角的位置,需抓住“二面角的平面角”的三个要素:(1)确定二面角的棱上一点;(2)经过这点分别在两个面内引射线;(3)所引的射线都垂直于棱.
平面角是直角的二面角叫做直二面角.
3.例题分析
例1 如图3,平面角为锐角的二面角 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,若
,若 ![]() 与
与 ![]() 所成角为
所成角为 ![]() ,求二面角
,求二面角 ![]() 的平面角.
的平面角.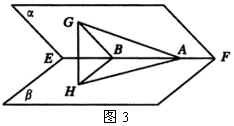
解:作 ![]() 于
于 ![]() ,作
,作![]() 于
于 ![]() ,连结
,连结 ![]() ,则
,则 ![]() ,
, ![]() 是二面角的平面角.
是二面角的平面角.
又 ![]() 是
是 ![]() 与
与 ![]() 所成的角,
所成的角,
设 ![]() ,
,
则 ![]() ,
, ![]() ,
, ![]() .
.
∴ ![]() .
.
例2 正三角形 ![]() 边长为10,
边长为10, ![]() 平面
平面 ![]() ,
, ![]() 、
、 ![]() 与平面
与平面 ![]() 的距离为4和2,
的距离为4和2, ![]() 、
、 ![]() 在平面
在平面 ![]() 的同侧,求:平面
的同侧,求:平面 ![]() 与平面
与平面 ![]() 所成的角
所成的角 ![]() .
.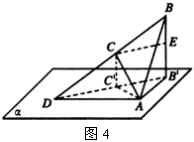
解:如图4.设 ![]() 、
、 ![]() 是
是 ![]() 、
、 ![]() 在平面
在平面 ![]() 上的射影,延长
上的射影,延长 ![]() 交平面
交平面 ![]() 于
于 ![]() ,
,
则平面 ![]() .
.
由已知可得 ![]() 、
、 ![]() 分别是
分别是 ![]() 和
和 ![]() 的中点.
的中点.
∴ ![]()
由 ![]() 得
得 ![]() .
.
又 ![]() ,故
,故 ![]() ,由三垂线逆定理得
,由三垂线逆定理得 ![]() .
.
由于 ![]() ,则
,则 ![]() .
.
∴ ![]() .
.
[演练反馈]
1.课本P36练习1,2,3,4.
2.二面角指的是(
)
A.两个平面相交所成的角
B.经过同一条直线的两个平面所组成的图形
C.从一条直线出发的两个半平面组成的图形
D.两个相交平面所夹的不大于 ![]() 的角
的角
3.已知△ ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 在平面
在平面 ![]() 内,△
内,△ ![]() 所在平面与面
所在平面与面 ![]() 成
成 ![]() 角,则△
角,则△ ![]() 在平面
在平面 ![]() 内的射影面积可能是(
)
内的射影面积可能是(
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4.已知二面角 ![]() 的平面角是锐角
的平面角是锐角 ![]() ,
, ![]() 内一点
内一点 ![]() 到
到 ![]() 的距离为3,点
的距离为3,点 ![]() 到棱
到棱 ![]() 的距离为4,那么
的距离为4,那么 ![]() 的值等于(
)
的值等于(
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
5.已知二面角 ![]() 的平面角为
的平面角为 ![]() ,
, ![]() ,若
,若 ![]() 到平面
到平面 ![]() 的距离为
的距离为 ![]() ,则
,则 ![]() 点在
点在 ![]() 上的射影
上的射影 ![]() 到平面
到平面 ![]() 的距离为________________.
的距离为________________.
6.自二面角内任意一点分别向两个面引垂线,则两垂线所成的角与二面角的平面角的关系是(
)
A.相等
B.互补
C.互余
D.无法确定
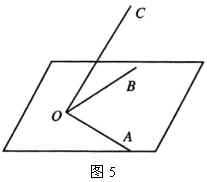
7.如图5, ![]() ,过点
,过点 ![]() 引
引 ![]() 所在平面的斜线
所在平面的斜线 ![]() ,
, ![]() 与
与 ![]() 、
、 ![]() 分别成
分别成 ![]() 、
、 ![]() 角,求二面角
角,求二面角 ![]() 的平面角的余弦值.
的平面角的余弦值.
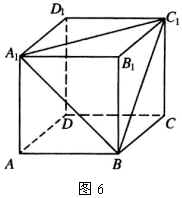
8.如图6,在正方体 ![]() 中,求二面角
中,求二面角 ![]() 的平面角的正切值.
的平面角的正切值.
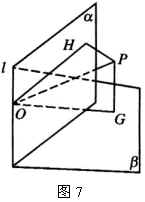
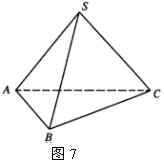
9.如图7,在 ![]() 的二面角
的二面角 ![]() 内有一点
内有一点 ![]() ,它到
,它到 ![]() 、
、 ![]() 面的距离分别为3和5,求
面的距离分别为3和5,求 ![]() 点到棱
点到棱 ![]() 的距离.
的距离.
[参考答案]
1.略. 2.C 3.D 4.C
5. ![]() 6.B
6.B
7.提示:在 ![]() 上任取一点
上任取一点 ![]() ,作
,作 ![]() 交
交 ![]() 于
于 ![]() 点,作
点,作 ![]() 交
交 ![]() 与
与 ![]() 点,令
点,令 ![]() ,则
,则 ![]() 即为所求,先在
即为所求,先在 ![]() △
△ ![]() 及△
及△ ![]() 中算出
中算出 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() ,再在
,再在 ![]() △
△ ![]() 中算出
中算出 ![]() .
.
8.提示:连结 ![]() 交
交 ![]() 于点
于点 ![]() ,连结
,连结 ![]() ,证明
,证明 ![]() 就是二面角
就是二面角 ![]() 的平面角.
的平面角.
9.提示:分别作 ![]() 、
、 ![]() 垂直于面
垂直于面 ![]() 、
、 ![]() 于点
于点 ![]() 、
、 ![]() ,证明
,证明 ![]() 面
面 ![]() ,令
,令 ![]() 交于
交于 ![]() 于点
于点 ![]() ,连结
,连结 ![]() 、
、 ![]() ,证明
,证明 ![]() ,
, ![]() ,
, ![]() 为所求.在△
为所求.在△ ![]() 中用余弦定理算出
中用余弦定理算出 ![]() .又
.又 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 共圆,可由正弦定理去算
共圆,可由正弦定理去算 ![]() .
.
[总结提炼]
求二面角的平面角,首先要选择一个合适的方案画出二面角(平臣式、直立式),其次要能够根据定义作出二面角的平面角,用三垂线定理作二面角的平面角是最常用的方法,用三垂线定理必须先找到一个参考平面,二面角的两个半平面之一往往就是参考平面,而三垂线定理的特点是斜线和射影同时垂直于面内的直线,这恰好符合二面角的平面角的两边同时垂直于棱的要求,最后要注意作、证、算的步骤安排,当然有时也直接按定义去作二面角的平面角.
布置作业:课本P39习题9.6 1,2,3,4,5.
板书设计:
|
1.二面角 例1 练习 2.二角面的平面角 例2 |
教学设计示例二
9.6 两个平面垂直的判定和性质 第二课时
教学目标:
1.理解两个平面垂直的定义.
2.掌握面面垂直的判定定理与性质定理.
3.能应用面面垂直的判定与性质解决简单问题.
教具准备:三角板、投影胶片.
教学过程:
[设置情境]
提问:
(1)竖电线杆时,电线杆所在的直线与地面应满足怎样的位置呢?
(2)为了让一面墙砌得稳固,不易倒塌,墙面所在的平面与地面又应该满足怎样的位置关系呢?
容易得出结论:电线杆与地面应该垂直,否则容易倾倒;如果墙面发生倾斜,墙就容易倒塌,所以砌墙时,不能让墙面倾斜.
(3)我们怎样用所学知识去描述“墙面不倾斜”这一事实呢?
[探索研究]
1.平面与平面垂直的定义
如果两个平面所成的二面角是直角,就说这两个平面互相垂直.
2.两个平面垂直的判定定理
提出问题:如果你是一个质检员,你怎样去检测、判断建筑中的一面墙和地面是否垂直呢?
(教师可鼓励学生结合自己的生活阅历大胆想象、猜测,并可用书作墙面、桌面作为地面进行模拟.学生不管想出何种方法,也不管其是否可行,教师都应给以表扬、鼓励并作出相应的分析.)
由上面的讨论分析,教师得出两个平面垂直的判定定理: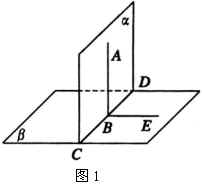
如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
已知: ![]() ,
,
![]() (图1).
(图1).
求证: ![]() .
.
证明:设 ![]() ,则由
,则由 ![]() 知,
知, ![]() 、
、 ![]() 共面.
共面.
∵ ![]() ,
, ![]() ,
,
∴ ![]() ,垂足为点
,垂足为点 ![]() .
.
在平面 ![]() 内过点
内过点 ![]() 作直线
作直线 ![]() ,则
,则 ![]() 是二面角
是二面角 ![]() 是直二面角.
是直二面角.
∴ ![]() .
.
3.两个平面垂直的性质
提问:为什么墙面和地面垂直的时候,墙体就不容易倒塌呢?先让学生思考,然后演示实验:将一本书放置在桌面上,且使书所在平面与桌面垂直.当书面沿书面与桌面的交线转动时,由物理学原理知,它会倒塌.
由此得到启发,让学生思考:如果两个平面互相垂直,那么在第一个平面内垂直于交线的直线,是否垂直于第二个平面呢?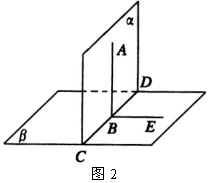
先让学生思考一段时间,然后分析:
如图2, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
求证: ![]() .
.
分析:在 ![]() 内作
内作 ![]() .
.
要证 ![]() ,只需证
,只需证 ![]() 垂直于
垂直于 ![]() 内的两条相交直线就行,而我们已经有
内的两条相交直线就行,而我们已经有 ![]() ,只需寻求另一条就够了,而我们还有
,只需寻求另一条就够了,而我们还有 ![]() 这个条件没使用,由
这个条件没使用,由 ![]() 定义,则
定义,则 ![]() 为直角,即有
为直角,即有 ![]() ,也就有
,也就有 ![]() ,问题也就得到解决.可由学生写出证明过程.
,问题也就得到解决.可由学生写出证明过程.
由上面的讨论,我们就得到了两个平面垂直的性质定理:
如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.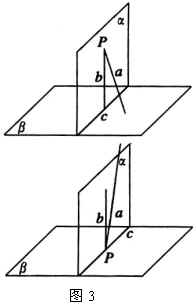
下面我们来看一下两个平面垂直的性质的另一个定理,也即课本的例2(P37).
如果两个平面互相垂直,那么经过第一个平面的一点垂直于第二个平面的直线,在第一个平面内.
已知: ![]() ,
, ![]() ,
, ![]() ,
, ![]() (图3).
(图3).
求证: ![]() .
.
证明:设 ![]() .过点
.过点 ![]() 在平面
在平面 ![]() 内作直线
内作直线 ![]() ,根据上面的定理有
,根据上面的定理有 ![]() .
.
因为经过一点只能有一条直线与平面 ![]() 垂直,所以直线
垂直,所以直线 ![]() 应与直线
应与直线 ![]() 重合.
重合.
∴ ![]() .
.
4.例题分析
例题 如图4, ![]() 是⊙
是⊙ ![]() 的直径,点
的直径,点 ![]() 是⊙
是⊙ ![]() 上的动点,过动点
上的动点,过动点 ![]() 的直线
的直线 ![]()
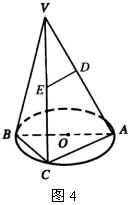 垂直于⊙
垂直于⊙ ![]() 所在平面,
所在平面, ![]() 、
、 ![]() 分别是
分别是 ![]() 、
、 ![]() 的中点,直线
的中点,直线 ![]() 与平面
与平面 ![]() 有什么关系?试说明理由.
有什么关系?试说明理由.
解:由 ![]() 垂直于⊙
垂直于⊙ ![]() 所在平面,知
所在平面,知 ![]() ,
, ![]() ,即
,即 ![]() 是二面角
是二面角 ![]() 的平面角.由
的平面角.由 ![]() 是直径上的圆周角,知
是直径上的圆周角,知 ![]() .因此,平面
.因此,平面 ![]() 平面
平面 ![]() .由
.由 ![]() 是△
是△ ![]() 两边中点连线,知
两边中点连线,知 ![]() ,故
,故 ![]() .由两个平面垂直的性质定理,知直线
.由两个平面垂直的性质定理,知直线 ![]() 与平面
与平面 ![]() 垂直.
垂直.
注意:本题也可以先推出 ![]() 垂直于平面
垂直于平面 ![]() ,再由
,再由 ![]() ,推出上面的结论.
,推出上面的结论.
[演练反馈]
1.如图5,在空间边形 ![]() 中,
中, ![]() 平面
平面 ![]() ,
, ![]() ,
, ![]() ,
, ![]() .求证:(1)
.求证:(1) ![]() ;(2)平面
;(2)平面 ![]() 平面
平面 ![]() .
.
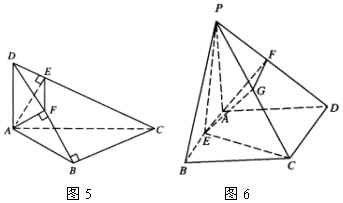
2.如图6, ![]() 是△
是△ ![]() 所在平面外一点,
所在平面外一点, ![]() ,
, ![]() ,
, ![]() .求证:平面
.求证:平面 ![]() 平面
平面 ![]() .
.
3.如图7, ![]() 垂直于矩形
垂直于矩形 ![]() 所在平面,
所在平面, ![]() 、
、 ![]() 分别是
分别是 ![]() 、
、 ![]() 的中点,二面角
的中点,二面角 ![]() 为
为 ![]() .求证:平面
.求证:平面 ![]() 平面
平面 ![]() .
.
[参考答案]
1.提示:由 ![]() ,
, ![]() ,得
,得 ![]() 面
面 ![]() ,从而面
,从而面 ![]() 面
面 ![]() ,又
,又 ![]() ,所以
,所以 ![]() 面
面 ![]() ,所以
,所以 ![]() ,得
,得 ![]() 面
面 ![]() .
.
2.提示:取 ![]() 中点
中点 ![]() ,连结
,连结 ![]() 、
、 ![]() .
. ![]() ,
, ![]() ,得
,得 ![]() .
.
3.提示:取 ![]() 中点
中点 ![]() ,连结
,连结 ![]() 、
、 ![]() ,证明:
,证明: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 面
面 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 面
面 ![]() ,
, ![]() 面
面 ![]() .
.
[总结提炼]
定义面面垂直是在建立在二面角的平面角的基础上的,理解面面垂直的判定与性质都要依赖面面垂直的定义.证明面面垂直要从寻找面的垂线入手,课本第37页上的例2也可以当作面面垂直的一条性质定理,在解题时注意应用.
布置作业:课本P39习题9.6 6,7,8,9,10.
板书设计:
|
1.两个平面垂直的判定 3.两个平面垂直性质之二 2.两个平面垂直的性质之一 4.例题 |
教学设计示例三
9.6 两个平面垂直的判定和性质 第三课时
教学目标:
1.巩固复习二面角的有关概念,进一步培养求二面角的平面角的能力.
2.巩固复习面面垂直的定义,熟练掌握面面垂直的判定与性质定理.
教具准备:三角板.
教学过程:
[复习回忆]
1.二面角的有关概念.
2.作二面角的平面角的一般方法.
3.两个平面垂直的判定定理.
4.两个平面垂直的性质定理(两个).
[探索研究]
例1 在平面四边形 ![]() 中,已知
中,已知 ![]() ,
, ![]() ,
, ![]() ,沿
,沿 ![]() 将四边形折成直二面角
将四边形折成直二面角 ![]() .
.
(1)求证:平面 ![]() 平面
平面 ![]() ;
;
(2)求平面 ![]() 与平面
与平面 ![]() 所成的角.
所成的角.
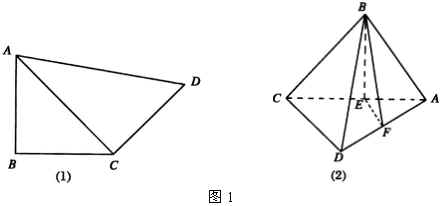
解:如图1,其中(1)是平面四边形,(2)是折后的立体图.
(1)证明:∵平面 ![]() 平面
平面 ![]() ,交线为
,交线为 ![]() ,
,
又∵ ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() .
.
∴ 
![]() 平面
平面 ![]() 平面
平面 ![]() .
.
(2)过点 ![]() 作
作 ![]() ,
, ![]() 为垂足,则
为垂足,则 ![]() 平面
平面 ![]() .又过点
.又过点 ![]() 在平面
在平面 ![]() 内作
内作 ![]() ,
, ![]() 为垂足,连结
为垂足,连结 ![]() .由三垂线定理可知
.由三垂线定理可知 ![]() .∴
.∴ ![]() 是二面角
是二面角 ![]() 的平面角.
的平面角.
∵点 ![]() 为
为 ![]() 中点,∴
中点,∴ ![]() .
.
又 ![]() ,
, ![]()
∴ ![]() .
.
![]() .
.
∴ ![]() .即平面
.即平面 ![]() 与平面
与平面 ![]() 所成的二面角为
所成的二面角为 ![]() .
.
点评:折叠问题要特别重视线与线的位置关系,有的在折叠前后保持不变,关于它们的计算,可以在平面图形中求得,如本题中 ![]() 在折叠前后不变,四边形的四条边的长也不变.所以,
在折叠前后不变,四边形的四条边的长也不变.所以, ![]() 、
、 ![]() 均可在平面四边形中求得,但有些量折叠前后会发生变化,如
均可在平面四边形中求得,但有些量折叠前后会发生变化,如 ![]() 折叠后不再是
折叠后不再是 ![]() ,点
,点 ![]() 和点
和点 ![]() 间的距离折叠后也变短了,已经变化了的量切不可用折叠前的数据进行计算.
间的距离折叠后也变短了,已经变化了的量切不可用折叠前的数据进行计算.
例2 如图2,在立体图 ![]() 中,
中, ![]() 底面
底面 ![]() ,
, ![]() ,
, ![]() 垂直平分
垂直平分 ![]() 且分别交
且分别交 ![]() 、
、 ![]() 于
于 ![]() 、
、 ![]() ,又
,又 ![]() ,
, ![]() ,求以
,求以 ![]() 为棱,以
为棱,以 ![]() 与
与 ![]() 为面的二面角的平面角的度数.
为面的二面角的平面角的度数.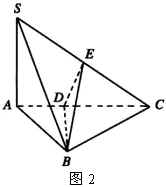
分析:由已给出的线面垂直关系及线线垂直关系,很容易发现 ![]() 平面
平面 ![]() ,∴
,∴ ![]() 就是所求二面角的平面角.
就是所求二面角的平面角.
解:由于 ![]() ,且
,且 ![]() 是
是 ![]() 的中点,因此
的中点,因此 ![]() 是等腰△
是等腰△ ![]() 的底边
的底边 ![]() 的中线,所以
的中线,所以 ![]() .
.
又已知 ![]() ,
, ![]() ,
,
∴ ![]() 面
面 ![]() ,∴
,∴ ![]() .
.
又∵ ![]() 底面
底面 ![]() ,
, ![]() 底面
底面 ![]() ,
,
∴ ![]() ,而
,而 ![]() .
.
∴ ![]() 平面
平面 ![]() .
.
∵ ![]() 平面
平面 ![]() 平面
平面 ![]() ,
,
∴ ![]() ,
, ![]() .
.
∴ ![]() 是所求二面角的平面角.
是所求二面角的平面角.
∵ ![]() 底面
底面 ![]() ,∴
,∴ ![]() ,
, ![]() .
.
设 ![]() ,则
,则 ![]() ,
, ![]() .
.
又因为 ![]() ,所以
,所以 ![]() .
.
在 ![]() △
△ ![]() 中,
中, ![]() ,
,
∴ ![]() ,∴
,∴ ![]() ,即二面角
,即二面角 ![]() 的平面角的度数为
的平面角的度数为 ![]() .
.
例3 如图3,在底面是直角梯形的立体图 ![]() 中,
中, ![]() ,
, ![]() 面
面 ![]() ,
, ![]() ,
, ![]() ,求面
,求面 ![]() 与面
与面 ![]() 所成的二面角的平面角的正切值.
所成的二面角的平面角的正切值.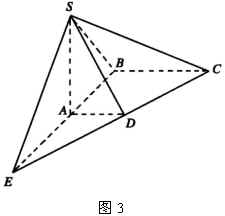
分析:这是一道求“二面角”的问题,常将两个平面的交线找出,再设法画出所求二面角的平面角.
解:延长 ![]() 、
、 ![]() 相交于点
相交于点 ![]() ,连结
,连结 ![]() ,则
,则 ![]() 是所求二面角的棱
是所求二面角的棱
∵ ![]() ,
, ![]() ,
,
∴ ![]() ,∴
,∴ ![]() .
.
∵ ![]() 面
面 ![]() ,得面
,得面 ![]() 面
面 ![]() ,
, ![]() 是交线.
是交线.
又 ![]() ,∴
,∴ ![]() 面
面 ![]() ,故
,故 ![]() 是
是 ![]() 在面
在面 ![]() 上的射影,∴
上的射影,∴ ![]() ,∴
,∴ ![]() 是所求的二面角的平面角.
是所求的二面角的平面角.
∵ ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]() .
.
即所求二面角的平面角的正切值为 ![]() .
.
[演练反馈]
1.如图4,△ ![]() 的边
的边 ![]() 在平面
在平面 ![]() 内,顶点
内,顶点 ![]() ,设△
,设△ ![]() 的面积为
的面积为 ![]() ,它在平面
,它在平面 ![]() 内射影的面积为
内射影的面积为 ![]() ,且平面
,且平面 ![]() 与△
与△ ![]() 所在平面所成的二面角的平面角为
所在平面所成的二面角的平面角为 ![]() (
( ![]() ).求证:
).求证: ![]() .
.
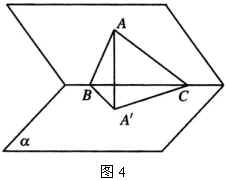
2.如图5,矩形 ![]() 中,
中, ![]() ,沿
,沿 ![]() 将△
将△ ![]() 折起后,使点
折起后,使点 ![]() 在平面
在平面 ![]() 上的射影恰好是
上的射影恰好是 ![]() 的中点
的中点 ![]() ,求二面角
,求二面角 ![]() 的大小.
的大小.
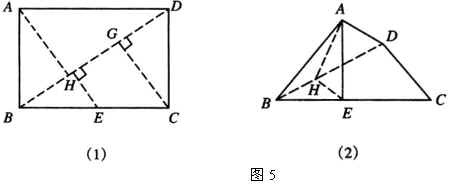
3.已知正方体 ![]() 中,
中, ![]() 是
是 ![]() 的中点,求平面
的中点,求平面 ![]() 与底面
与底面 ![]() 所成二面角的平面角的正弦值(图6).
所成二面角的平面角的正弦值(图6).
[参考答案]
1.提示:作 ![]() 于点
于点 ![]() ,则
,则 ![]() 就是△
就是△ ![]() 的面积,作
的面积,作 ![]() 于点
于点 ![]() ,连结
,连结 ![]() ,证
,证 ![]() ,
, ![]() ,
, ![]() .
.
2.提示:作 ![]() 于点
于点 ![]() ,连结
,连结 ![]() ,证明
,证明 ![]() ,
, ![]() 为所求.
为所求. ![]() ,
, ![]() .
.
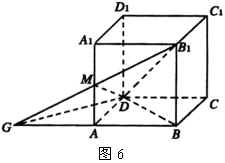
3.分析:延长 ![]() 交
交 ![]() 的延长线于
的延长线于 ![]() ,连结
,连结 ![]() ,∵
,∵ ![]() ,∴
,∴ ![]()
解法一:∵ ![]() ,
, ![]() ,
,
由三垂线定理,得 ![]() .
.
![]() 为二面角的平面角.
为二面角的平面角.
解得 ![]() .
.
另介绍用射影面积公式解.
如果△ ![]() 所在平面
所在平面 ![]() 与平面
与平面 ![]() 所成的二面角的平面角为
所成的二面角的平面角为 ![]() ,且△
,且△ ![]() 在平面
在平面 ![]() 内的射影为△
内的射影为△ ![]() ,则有
,则有![]() .
.
解法二:△ ![]() 在底面
在底面 ![]() 上的射影是△
上的射影是△ ![]() ,设正方体的棱长为2,则
,设正方体的棱长为2,则 ![]() ,
, ![]() ,设所求的平面角为
,设所求的平面角为 ![]() ,则
,则 ![]() ,∴
,∴ ![]() .
.
[总结提炼]
处理折叠问题,关键是认清折叠前后的不变量,当一个二面角的棱在图形中未显示时,那么求这个二面角的首要任务便是找到棱,这往往要用到公理1或公理2,利用 ![]() 来求二面角的平面角的方法很特殊,对于有些问题相当方便,请大家注意记忆.
来求二面角的平面角的方法很特殊,对于有些问题相当方便,请大家注意记忆.
布置作业:
1.课本P39习题9.6 11,12,13,14.
2.一条长为 ![]() 的线段
的线段 ![]() 夹在互相垂直的两个平面
夹在互相垂直的两个平面 ![]() 、
、 ![]() 之间,
之间, ![]() 与
与 ![]() 所成的角为
所成的角为 ![]() ,与
,与 ![]() 所成角为
所成角为 ![]() ,且
,且 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 、
、 ![]() 是垂足.求平面
是垂足.求平面 ![]() 与平面
与平面 ![]() 所成的角.
所成的角.
[参考答案]
1.略.
2.解:如图7.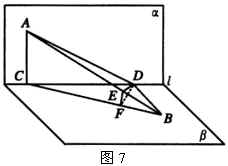
连结 ![]() 、
、 ![]() ,可证
,可证 ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() .
.
在 ![]() △
△ ![]() 中,
中, ![]() ,在
,在 ![]() △
△ ![]() 中,
中, ![]() .
.
在 ![]() △
△ ![]() 中,可求出
中,可求出 ![]() .
.
又作 ![]() 于
于 ![]() ,作
,作 ![]() ,交
,交 ![]() 于
于 ![]() ,则
,则 ![]() 就是二面角
就是二面角 ![]() 的平面角,由
的平面角,由 ![]() 平面
平面 ![]() ,得
,得 ![]() .
.
又 ![]() ,∴
,∴ ![]() 平面
平面 ![]() .
.
∴ ![]() .
.
∴ ![]() 即为所求二面角的平面角.
即为所求二面角的平面角.
在 ![]() △
△ ![]() 中,
中, ![]() ,
,
在 ![]() △
△ ![]() 中,
中, ![]() ,
,
在 ![]() △
△ ![]() 中,
中, ![]() ,
,
∴ ![]() ,即平面
,即平面 ![]() 与平面
与平面 ![]() 所成的角为
所成的角为 ![]() 或
或 ![]() .
.
板书设计:
|
1.例1 3.例3 2.例2 4.练习 |