 设为首页
设为首页
 加入收藏
加入收藏
教学设计示例一
9.2 空间直线 第一课时
教学目标
1.了解空间两条直线的位置关系.
2.学习掌握公理4.
3.理解掌握等角定理.
4.能应用公理4及等角定理解决简单问题.
教具准备:投影仪(胶片)、三角板.
教学过程
[设置情景]
(1)在同一平面内,两条直线有几种位置关系?(两种:平行、相交),那么在空间,两条直线有几种位置关系呢?
(2)在同一平面内,平行于同一条直线的两直线平行,在空间中此结论仍成立吗?
[探索研究]
1.空间两条直线的位置关系
空间直线的三种位置关系在现实中大量存在,在初中几何里已经介绍了空间的两条直线有以下三种位置关系:
(1)相交直线—有且仅有一个公共点.
(2)平行直线—在同一个平面内,没有公共点.
(3)异面直线—不同在任何一个平面内,没有公共点.
教师可出示立体几何模型,例如正方体模型,指出空间两条直线的各种位置关系.也可以教室内墙与墙的交线为例.
2.平行直线
(1)复习引入
在初中几何里我们已知道,在同一个平面内,如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
教师提问:对于空间的三条直线,是否也有这样的规律?
(2)导入新课
在教室内,大家一起找一找墙的交线有无不在同一平面内的三条直线两两平行的?在教师指导下找出.
我们把上述规律作为本章的第4个公理.
公理4 平行于同一条直线的两条直线互相平行.
公理4也可以用符号表示为:设 ![]() 、
、 ![]() 、
、 ![]() 为直线,
为直线, ![]()
![]() 、
、 ![]() 、
、 ![]() 三条直线两两平行,可以记为
三条直线两两平行,可以记为 ![]() .
.
例1 已知四边形 ![]() 是空间四边形(四个顶点不共面的四边形叫做空间四边形),
是空间四边形(四个顶点不共面的四边形叫做空间四边形), ![]() 、
、 ![]() 分别是边
分别是边 ![]() 、
、 ![]() 的中点,
的中点, ![]() 分别是边
分别是边 ![]() 上的点,且
上的点,且 ![]() ,求证:四边形
,求证:四边形 ![]() 有一组对边平行但不相等.
有一组对边平行但不相等.
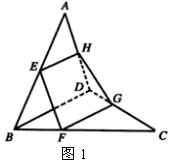
证明:如图1,连结 ![]() .
.
∵ ![]() 是
是 ![]() 的中位线.
的中位线.
∴ ![]() ,
, ![]() .
.
又在 ![]() 中,
中, ![]() ,
,
∴ ![]() ,
, ![]() .
.
根据公理4, ![]() .
.
又 ![]() ,
,
∴四边形 ![]() 的一组对边平行但不相等.
的一组对边平行但不相等.
由公理4,我们可以推出下面的结论.
定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等.
例2 已知: ![]() 和
和 ![]() 的边
的边 ![]() ,
, ![]() ,并且方向相同(即向量
,并且方向相同(即向量 ![]() 与
与 ![]() ,
, ![]() 与
与 ![]() 的方向相同).
的方向相同).
求证: ![]() .
.
证明:对于 ![]() 和
和 ![]() 都在同一平面内的情况,用初中几何知识可证明,下面我们证明两个角不在同一平面内的情况.
都在同一平面内的情况,用初中几何知识可证明,下面我们证明两个角不在同一平面内的情况.
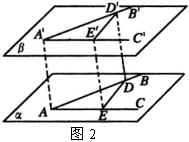 如图2,在
如图2,在 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 上分别取
上分别取 ![]() 、
、 ![]() ,连结
,连结 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() .
.
∵ ![]() ,
, ![]() .
.
∴四边形 ![]() 是平行四边形.
是平行四边形.
∴ ![]() .
.
同理 ![]() .
.
根据公理4,可得 ![]() .
.
又可得 ![]() ,
,
∴四边形 ![]() 是平行四边形.
是平行四边形.
∴ ![]() .于是
.于是 ![]()
∴ ![]() .
.
把上面两个角的两边反向延长,就得出下面的推论:
推论 如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.
注意:对于由平面图形得出的结论,有些可以推广到立体图形中,例如上面的定理和推论对于平面图形都成立,现在经证明可知对于立体图形也成立.但是,并非所有关于平面图形成立的结论,对于立体图形都适用.例如,在同一平面内,垂直于同一条直线的两条直线互相平行,但在空间里没有这样的结论.因此,一般地说,要把关于平面图形的结论推广到立体图形中,必须经过证明.
[演练反馈]
1.空间两直线平行是指它们( )
A.无交点 B.共面且无交点
C.和同一条直线垂直 D.以上都不对
2.在空间,如果一个角的两边与另一个角的两边分别平行,则这两个角( )
A.相等 B.互补
C.相等或互补 D.既不相等也不互补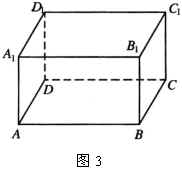
3.如图3, ![]() 是长方体的一条棱,这个长方体中与
是长方体的一条棱,这个长方体中与 ![]() 异面的棱共有( )
异面的棱共有( )
A.3条 B.4条 C.5条 D.6条
4.设直线 ![]() 、
、 ![]() 分别是长方体的相邻两个面的对角线所在的直线,则
分别是长方体的相邻两个面的对角线所在的直线,则 ![]() 与
与 ![]() ( )
( )
A.平行 B.相交
C.是异面直线 D.可能相交,可能异面
5.一条直线与两条平行线中的一条是异面直线,那么它与另一条的位置关系是( )
A.相交 B.异面 C.平行 D.相交或异面
6.两条异面直线是指( )
A.空间两条没有公共点的直线
B.平面内一直线与这个平面外的一直线
C.分别在两个平面内的两条直线
D.不同在任何一个平面内的两条直线
7.课本P11练习1.
8.课本P12练习2.
[参考答案]
1.B 2.C 3.B 4.D 5.D 6.D
7.理由依据为公理4.
8.利用平行关系的传递性证明 ![]() ,然后由平行四边形的性质得
,然后由平行四边形的性质得 ![]() ,
, ![]() ,
, ![]() ,故得
,故得 ![]() .
.
[总结提炼]
[学生回答,教师补充完善.]
1.两条直线的空间位置关系及它们的定义.
2.公理4.
3.等角定理及其推论.
(四)布置作业
课本P14习题9.2 1,2,3,4,5.
[参考答案]
略.
(五)板书设计
|
1.位置关系 2.公理4 3.例题 |
定理 推论 |
练习 |
教学设计示例二
9.2 空间直线 第二课时
教学目标
1.理解异面的定义,会画出两条异面直线.
2.理解异面直线所成的角,异面直线的公垂线及距离等概念.
3.能利用异面直线所成的角及异面直线间的距离等概念去求两条异面直线所成的角及两条异面直线间的距离.
4.初步了解反证法.
教具准备:投影仪(胶片)、三角板.
教学过程:
[设置情境]
两条平行线之间可以用距离度量它们的位置关系,两条相交直线可以用夹角来描述它们的位置关系,那么怎么描述两条异面直线的关系呢,它们之间存在着夹角和距离吗?
[探索研究]
1.异面直线的定义
不同在任何一个平面内的两条直线,叫做异面直线.
异面直线是指两条直线不能同在任何一个平面内,而不能由 ![]() 、
、 ![]() 就说
就说 ![]() 一定是异面直线,这是因为在上述情况下,还可能有
一定是异面直线,这是因为在上述情况下,还可能有 ![]() 且
且 ![]() .两条直线是异面直线,等价于两条直线既不相交也不平行.
.两条直线是异面直线,等价于两条直线既不相交也不平行.
2.异面直线的画法
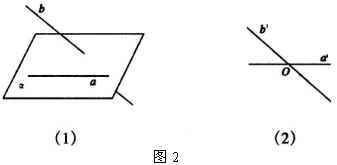
表示异面直线时,以一个或两个平面衬托以显示出它们不共面的特点.如图1
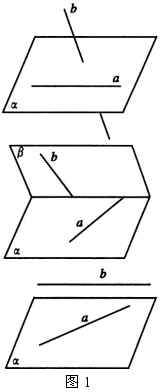
3.两异面直线所成的角
过空间任意一点,分别作两条异面直线的平行线,则这两条相交直线所成的锐角(或直角)叫做这两条异面直线所成的角.
如图2(l),直线 ![]() 、
、 ![]() 是异面直线,图2(2)中
是异面直线,图2(2)中 ![]() ,
, ![]() ,
, ![]() .则
.则 ![]() 和
和 ![]() 所成的锐角(或直角)就是
所成的锐角(或直角)就是 ![]() 、
、 ![]() 所成的角.
所成的角.
4.异面直线互相垂直
如果两条异面直线所成的角是直角,我们就说这两条异面直线互相垂直.异面直线 ![]() 和
和 ![]() 互相垂直,也记作
互相垂直,也记作 ![]() .
.
以后,我们讲两条直线垂直时,有时交垂直与异面垂直两种情况.异面直线所成的角范围是: ![]() .
.
5.两条异面直线的公垂线与距离
和两条异面直线都垂直相交的直线,叫做两条异面直线的公垂线.
两条异面直线的公垂线在这两条异面直线间的线段(公垂线段)的长度,叫做两条异面直线的距离.
6.例题分析
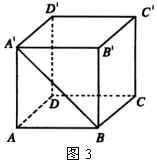
例1 设图3中的正方体的棱长为 ![]() ,(1)求直线
,(1)求直线 ![]() 和
和 ![]() 所成的角的大小;(2)求异面直线
所成的角的大小;(2)求异面直线 ![]() 和
和 ![]() 的距离.
的距离.
解:(1)∵ ![]()
∴ ![]() 和
和 ![]() 所成的锐角就是
所成的锐角就是 ![]() 和
和 ![]() 所成的角.
所成的角.
∵ ![]()
∴ ![]() 和
和 ![]() 所成的角是
所成的角是 ![]() .
.
(2)  .
.
对于任意两条异面直线,它们的公垂线有且仅有一条(证明略).高考中,求异面直线的距离,只要求会已给出公垂线的距离的计算.
例2 求证:过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线.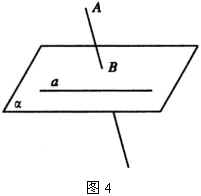
已知: ![]() ,
, ![]() ,
, ![]() ,
, ![]() (图4).
(图4).
求证:直线 ![]() 和
和 ![]() 是异面直线.
是异面直线.
证明:用反证法证明.假设直线 ![]() 和
和 ![]() 共面,即有平面
共面,即有平面 ![]() 使
使 ![]() ,
, ![]() ,于是
,于是 ![]() ,
, ![]() .
.
∵ ![]() ,
, ![]() ,
, ![]() .
.
∴过 ![]() 和
和 ![]() 有且仅有一个平面,即平面
有且仅有一个平面,即平面 ![]() .于是,
.于是, ![]() 和
和 ![]() 是同一平面,即
是同一平面,即 ![]() .
.
由假设知 ![]() ,可知
,可知 ![]() ,这与已知
,这与已知 ![]() 矛盾.
矛盾.
∴直线 ![]() 和
和 ![]() 是异面直线.
是异面直线.
[演练反馈]
1.若 ![]() 、
、 ![]() 是异面直线,
是异面直线, ![]() 、
、 ![]() 是异面直线,则
是异面直线,则 ![]() 、
、 ![]() 的位置关系不可能是( )
的位置关系不可能是( )
A.相交直线 B.平行直线
C.异面直线 D.以上结论都不对
2.没有公共点的两条直线的位置关系是( )
A.异面 B.平行
C.异面或平行 D.不确定
3.下列说法中正确的是( )
A.![]()
![]() ,则
,则 ![]() 与
与 ![]() 是异面直线
是异面直线
B.![]() 与
与 ![]() 异面,
异面, ![]() 与
与 ![]() 异面,则
异面,则 ![]() 与
与 ![]() 异面
异面
C.![]() 、
、 ![]() 不同在平面
不同在平面 ![]() 内,则
内,则 ![]() 与
与 ![]() 异面
异面
D.![]() 、
、 ![]() 不同在任何一个平面内,
不同在任何一个平面内, ![]() 与
与 ![]() 异面
异面
4.异面直线 ![]() 、
、 ![]() 分别在平面
分别在平面 ![]() 和
和 ![]() 内,若
内,若 ![]() ,则直线
,则直线 ![]() 必定( )
必定( )
A.分别与 ![]() 、
、 ![]() 相交
相交
B.与 ![]() 、
、 ![]() 都不相交
都不相交
C.至多与 ![]() 、
、 ![]() 中的一条相交
中的一条相交
D.至少与 ![]() 、
、 ![]() 中的一条相交
中的一条相交
5.在正方体 ![]() 中,与对角线
中,与对角线 ![]() 异面的棱共有______条.
异面的棱共有______条.
6. ![]() 、
、 ![]() 是异面直线,
是异面直线, ![]() ,则
,则 ![]() 与
与 ![]() 的位置关系是__________.
的位置关系是__________.
[参考答案]
1.D 2.C 3.D 4.D 5.6 6.相交或异面
[总结提炼]
画两条异面直线必须用一个平面去衬托,异面直线所成角的定义的合理性是由等角定理保证的,要求两条异面直线间的距离必须先找到这两条异面直线的公垂线,考纲中只要求会计算已经给出公垂线段的两异面直线间的距离,反证法一般都是在正面证明不方便的情况下使用的.
(四)布置作业
课本P15习题9.2 6,7,8,9,10.
(五)板书设计
|
1.复习 例1 例2 2.异面直线 (1)定义 (2)画法 (3)所成的角 (4)垂直 (5)公垂线和距离 |
教学设计示例三
9.2 空间直线 第三课时
教学目标:
1.巩固复习异面直线,异面直线所成的角及异面直线间的距离等概念
2.会根据概念求异面直线所成的角以及两条异面直线间的距离.
教具准备:投影仪(胶片)、三角板.
教学过程:
[复习引入]
(1)空间两直线的位置关系,公理4.
(2)异面直线的概念.
(3)异面直线所成的角和异面直线间的距离的概念.
(4)空间等角定理及推论.
[探索研究]
例1 如图1,已知平面 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求证:
,求证: ![]() 和
和 ![]() 是异面直线.
是异面直线.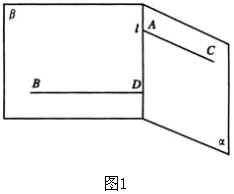
证明:(反证法)
假设 ![]() 、
、 ![]() 在同一平面
在同一平面 ![]() 内.
内.
∵ ![]() 、
、 ![]() 、
、 ![]() 既在
既在 ![]() 内又在
内又在 ![]() 内,且
内,且 ![]() 、
、 ![]() 、
、 ![]() 三点不
三点不
共线.
∴ ![]() 与
与 ![]() 重合.
重合.
又 ![]() 、
、 ![]() 、
、 ![]() 既在
既在 ![]() 内又在
内又在 ![]() 内.
内.
同理, ![]() 与
与 ![]() 重合.
重合.
∴ ![]() 与
与 ![]() 重合.但这与已知
重合.但这与已知 ![]() 相矛盾,所以假设不成立.
相矛盾,所以假设不成立.
故 ![]() 与
与 ![]() 是异面直线.
是异面直线.
例2 如图2,在正方体 ![]() 中,
中, ![]() 为上底面中心,求下列异面直线所成的角:
为上底面中心,求下列异面直线所成的角:
(1) ![]() 与
与 ![]() ;
;
(2) ![]() 与
与 ![]() ;
;
(3) ![]() 与
与 ![]() .
.
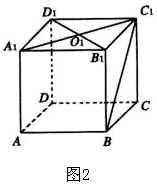
解:(1)平移 ![]() 到
到 ![]() ,则
,则 ![]() 为所求.而
为所求.而 ![]() 为等边三角形,∴
为等边三角形,∴ ![]() .
.
(2)平移 ![]() 到
到 ![]() (
( ![]()
![]() 分别为
分别为 ![]() 与
与 ![]() 的中点,)用公理4证明
的中点,)用公理4证明 ![]() ,从而
,从而 ![]() ,再证
,再证 ![]() ,得证
,得证 ![]() 为平行四边形,进而发现是菱形,设
为平行四边形,进而发现是菱形,设 ![]() 与
与 ![]() 交点
交点 ![]() ,则
,则 ![]() 与
与 ![]() 所成的角为所求∵
所成的角为所求∵ ![]() ∴
∴ ![]() 与
与 ![]() 所成角为
所成角为 ![]() .
.
(3)平移 ![]() 到
到 ![]() ,则
,则 ![]() 为所求,解
为所求,解 ![]() ,此三角形为等腰三角形(∵
,此三角形为等腰三角形(∵ ![]() ),
), 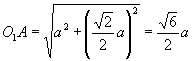 ,
,
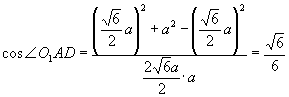 .
.
∴ ![]() .
.
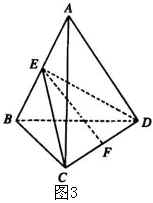 例3 如图3,空间四边形
例3 如图3,空间四边形 ![]() 边长均为
边长均为 ![]() ,连对角线
,连对角线 ![]() 、
、 ![]() ,且
,且 ![]() ,
, ![]() 、
、 ![]() 分别为
分别为 ![]() 、
、 ![]() 的中点.
的中点.
(1)证明: ![]() 是异面直线
是异面直线 ![]() 、
、 ![]() 的公垂线;
的公垂线;
(2)求异面直线 ![]() 与
与 ![]() 的距离
的距离
解:(1)连 ![]() 、
、 ![]() ,由题设,知
,由题设,知 ![]() ,
,
∴ ![]()
在等腰 ![]() 中,
中, ![]() 是
是 ![]() 的中线,
的中线,
∴ ![]() .
.
同理可证, ![]() .
.
∴ ![]() 与异面直线
与异面直线 ![]() 、
、 ![]() 相交且垂直,即
相交且垂直,即 ![]() 是异面直线
是异面直线 ![]() 与
与 ![]() 的公垂线.
的公垂线.
(2)在 ![]() 中,
中, ![]() ,
,![]() ,
,
∴ ![]() .
.
因此, ![]() 与
与 ![]() 间的距离为
间的距离为 ![]() .
.
[演练反馈]
1.如图4,在正方体中, ![]() 、
、 ![]() 分别为
分别为 ![]() 、
、 ![]() 上的点,且
上的点,且 ![]() ,求
,求 ![]() 与
与 ![]() 所成角的余弦值.
所成角的余弦值.
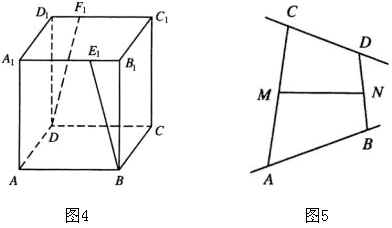
2.如图5, ![]() 是异面直线
是异面直线 ![]() 上的点,线段
上的点,线段 ![]() ,
, ![]() 为
为 ![]() 的中点,
的中点, ![]() 为
为 ![]() 的中点,
的中点, ![]() ,求异面直线
,求异面直线 ![]() 所成角的余弦值.
所成角的余弦值.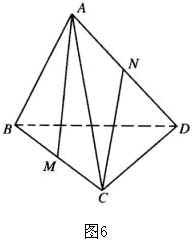
3.如图6,在空间四边形 ![]() 中,
中, ![]() ,
, ![]() 分别是
分别是 ![]() 和
和 ![]() 的中点,求异面直线
的中点,求异面直线 ![]() 和
和 ![]() 所成角的余弦值.
所成角的余弦值.
[参考答案]
1.提示:在棱 ![]() 上取
上取 ![]() ,取
,取 ![]() 中点
中点 ![]() ,连结
,连结 ![]() ,用公理4证明出
,用公理4证明出 ![]() ,得
,得 ![]() 为平行四边形,从而
为平行四边形,从而 ![]() ,再由
,再由 ![]() 得到
得到 ![]() (公理4),则
(公理4),则 ![]() 即为所求,最后用余弦定理的
即为所求,最后用余弦定理的 ![]() .
.
2.提示:取 ![]() 中点
中点 ![]() ,连
,连 ![]() ,易证
,易证 ![]() ,
, ![]() .则
.则 ![]() 与
与 ![]() 所成的角即为所求,在
所成的角即为所求,在 ![]() 中用余弦定理算出
中用余弦定理算出 ![]() ,而
,而 ![]() 与
与 ![]() 所成的角为
所成的角为![]() 的补角,所以结果应为
的补角,所以结果应为 ![]() .
.
3.提示:连结 ![]() ,取其中点
,取其中点 ![]() ,连
,连 ![]() 、
、 ![]() ,则
,则 ![]() ,∴
,∴ ![]() (或其补角)为异面直线
(或其补角)为异面直线 ![]() 与
与 ![]() 所成的角,在
所成的角,在 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,∴
,∴ ![]() ,即异面直线
,即异面直线 ![]() 和
和 ![]() 所成角的余弦值为
所成角的余弦值为 ![]() .
.
[总结提炼]
在作异面直线所成的角时,顶点往往选择在其中一条直线上,而且常常是该线段的端点或中点,在构成角的过程中,常常让其中一条线不动,另一条线沿着某个平面滑动(平移),直到两线相交,在计算异面直线所成的角时,要注意按“作→证→算”的步骤来进行.
(四)布置作业
1.和两异面直线都垂直的直线( )
A.不一定存在 B.仅有一条
C.有两条 D.有无数条
2.空间四边形 ![]() 的各边长均为
的各边长均为 ![]() 且对角线
且对角线 ![]() ,
, ![]() 分别是
分别是 ![]() 的中点,求
的中点,求 ![]() 与
与 ![]() 所成的角.
所成的角.
3.在棱长为 ![]() 的正方体
的正方体 ![]() 中,
中,
(1)求 ![]() 与
与 ![]() 所成的角;
所成的角;
(2)若 ![]() 分别是
分别是 ![]() 的中点,求
的中点,求 ![]() 与
与 ![]() 所成角的余弦值;
所成角的余弦值;
(3) ![]() 与
与 ![]() 的距离.
的距离.
[参考答案]
1.D 2. ![]()
3.略解:(1) ![]() 为
为 ![]() 与
与 ![]() 的夹角,在
的夹角,在 ![]() 中,
中, ![]() ,∴
,∴ ![]() .
.
(2)取 ![]() 中点
中点 ![]() ,连
,连 ![]() ,则
,则 ![]() ,∴
,∴ ![]() 为所求,在
为所求,在 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .
.
(3) ![]() .
.
(五)板书设计
|
例1 例3 练习 例2 |