 设为首页
设为首页
 加入收藏
加入收藏
教学设计示例(一)
教学目标
1.掌握抛物线的几何性质、能根据抛物线的几何性质画出抛物线图形;
2.能利用抛物线的几何性质解决有关问题.
教学过程
【情境设置】
由一名学生回答,教师板书.
问题 抛物线的标准方程是怎样的?答为:抛物线的标准方程是
![]() .
.
与椭圆、双曲线一样,通过抛物线的标准方程可以研究它的几何性质.
下面我们根据抛物线的标准方程: ![]() 来研究它的几何性质.
来研究它的几何性质.
【探索研究】
1.抛物线的几何性质
(1)范围
因为 ![]() ,由方程可知
,由方程可知 ![]() ,所以抛物线在
,所以抛物线在 ![]() 轴的右侧,当
轴的右侧,当 ![]() 的值增大时,
的值增大时, ![]() 也增大,这说明抛物线向右上方和右下方无限延伸.
也增大,这说明抛物线向右上方和右下方无限延伸.
(2)对称性
以 ![]() 代
代 ![]() ,方程不变,所以抛物线关于
,方程不变,所以抛物线关于 ![]() 轴对称.我们把抛物线的对称轴叫做抛物线的轴.
轴对称.我们把抛物线的对称轴叫做抛物线的轴.
(3)顶点
抛物线与它的轴的交点叫做抛物线的顶点,在方程中,当 ![]() 时
时 ![]() ,因此抛物线的顶点就是坐标原点.
,因此抛物线的顶点就是坐标原点.
(4)离心率
抛物线上的点与焦点的距离和它到准线的距离的比,叫做抛物线的离心率,由抛物线的定义可知 ![]()
其他三种标准方程抛物线的几何性质可类似地求得,教师用小黑板给出来表让学生填写.
|
标准方程 |
图形 |
顶点 |
对称轴 |
焦点 |
准线 |
离心率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
再向学生提出问题:与椭圆、双曲线的几何性质比较,抛物线的几何性质有什么特点?
学生和教师共同小结:
(1)抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;
(2)抛物线只有一条对称轴,没有对称中心;
(3)抛物线只有一个顶点、一个焦点、一条准线;
(4)抛物线的离心率是确定的,为1.
【例题分析】
例1 已知抛物线关于 ![]() 轴对称,它的顶点在坐标原点,并且经过点
轴对称,它的顶点在坐标原点,并且经过点 ![]() ,求它的标准方程,并用描点法画出图形.
,求它的标准方程,并用描点法画出图形.
求标准方程,请一名学生演板,教师予以纠正.画图可由教师讲解,步骤如下:
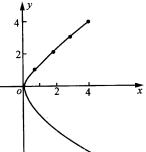 由求出的标准方程
由求出的标准方程
![]() ,变形为
,变形为 ![]() ,根据
,根据 ![]() 计算抛物线在
计算抛物线在 ![]() 的范围内几个点的坐标,得
的范围内几个点的坐标,得
|
|
0 |
1 |
2 |
3 |
4 |
…… |
|
|
0 |
1 |
2.8 |
3.5 |
4 |
…… |
描点画出抛物线的一部分,再利用对称性,就可以画出抛物线的另一部分(如图 ).
然后说明利用抛物线的通性,能够方便地画出反映抛物线基本特征的草图.
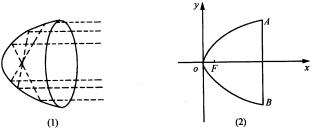
例2 探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处.已知灯口圆的直径为 ![]() ,灯深
,灯深 ![]() ,求抛物线的标准方程和焦点位置.
,求抛物线的标准方程和焦点位置.
解:如图,在探照灯的轴截面所在平面内建立直角坐标系,使反光镜的顶点(即抛物线的顶点)与原点重合, ![]() 轴垂直于灯口直径.
轴垂直于灯口直径.
抛物线的标准方程为 ![]() ,由已知条件可得点
,由已知条件可得点 ![]() 的坐标是(40,30)且在抛物线上,代入方程得:
的坐标是(40,30)且在抛物线上,代入方程得:
![]() ,
, ![]()
所以所求抛物线的标准方程为 ![]() ,焦点坐标是
,焦点坐标是 ![]() .
.
(三)随堂练习
1.求适合下列条件的抛物线方程
①顶点在原点,关于 ![]() 轴对称,并且经过点
轴对称,并且经过点 ![]()
②顶点在原点,焦点是 ![]()
③顶点在原点,准线是 ![]()
④焦点是 ![]() ,准线是
,准线是 ![]()
2.一条隧道的顶部是抛物拱形,拱高是 ![]() m,跨度是
m,跨度是 ![]() m,求拱形的抛物线方程
m,求拱形的抛物线方程
答案:1.① ![]() ②
② ![]() ③
③ ![]() ④
④ ![]()
2. ![]() (要选建立坐标系)
(要选建立坐标系)
(四)总结提炼
抛物线的性质和椭圆、双曲线比较起来,差别较大.它的离心率等于1;它只有一个焦点、一个顶点、一条对称轴、一条准线;它没有中心,也没有渐近线.
(五)布置作业
1.顶点在原点、焦点在 ![]() 轴上,且过点
轴上,且过点 ![]() 的抛物线方程是( )
的抛物线方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.若抛物线 ![]() 上横坐标为6的点到焦点的距离为8,则焦点到准线的距离为(
)
上横坐标为6的点到焦点的距离为8,则焦点到准线的距离为(
)
A.1 B.2 C.4 D.6
3.若垂直于 ![]() 轴的直线交抛物线
轴的直线交抛物线 ![]() 于点
于点 ![]() ,且
,且 ![]() ,则直线
,则直线 ![]() 的方程为______.
的方程为______.
4.抛物线形拱桥,当水面宽 ![]() 时,水面离拱顶为
时,水面离拱顶为 ![]() ,若水下降
,若水下降 ![]() ,则此时水面宽为___________.
,则此时水面宽为___________.
5.抛物线的顶点是双曲线 ![]() 的中心,而焦点是双曲线的左顶点,求抛物线方程.
的中心,而焦点是双曲线的左顶点,求抛物线方程.
6.若抛物线 ![]() 上一点
上一点 ![]() 到准线及对称轴的距离分别是10和6,求
到准线及对称轴的距离分别是10和6,求 ![]() 的横坐标及抛物线方程.
的横坐标及抛物线方程.
答案:1.B 2.C 3. ![]() 4.
4. ![]() 5.
5. ![]() 6.9,
6.9, ![]()
(六)板书设计
|
8.6 抛物线的简单几何性质(一) |
||
|
一、抛物线的几何性质 列表 |
二、例题分析 例1 |
例2 练习 总结 |
教学设计示例(二)
教学目标
1.进一步掌握应用抛物线的几何性质,来解决有关问题.
2.掌握直线与抛物线的位置关系,能综合应用有关知识解决抛物线的综合问题.
教学过程
【复习引入】
问:抛物线的标准方程有几种形式?抛物线的几何性质包括哪些内容?
答:抛物线的标准方程有四种不同的形式,其几何性质包括范围,对称性、顶点、离心率、准线方程等.
可利用投影仪展示抛物线标准方程的几何性质.
【例题分析】
例1 正三角表的一个顶点位于坐标原点,另外两个顶点在抛物线
![]() 上,求这个正三角形的边长.
上,求这个正三角形的边长.
分析:正三角表和抛物线都是轴对称圆形,如果能证明 ![]() 轴是它们的公共对称轴,则易解,而学生往往忽略了它的证明,可教师一边分析一边讲解.
轴是它们的公共对称轴,则易解,而学生往往忽略了它的证明,可教师一边分析一边讲解.
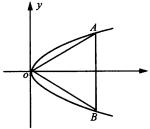
解:如图 ,设正三角形 ![]() 的顶点
的顶点 ![]() 在抛物线上,且它们坐标分别为
在抛物线上,且它们坐标分别为 ![]() 和
和 ![]() 则:
则: ![]() ,
, ![]()
又
![]() 所以:
所以: ![]()
 即:
即: ![]() ,
, ![]()
![]() ,
, ![]()
由此可得 ![]() ,即线段
,即线段 ![]() 关于
关于 ![]() 轴对称.
轴对称.
由于 ![]() 垂直于
垂直于 ![]() 轴,且
轴,且 ![]()
![]() ,而
,而 ![]() ,
, ![]()
![]()
于是 ![]()
点评:(1)求边长并不困难,往往会直观上承认抛物线与三角形的对称轴是公共的而忽略了它的证明.
(2)可由 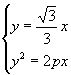 解得
解得 ![]() 或
或 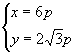 得
得 ![]()
![]()
(3)引申,求例1正三角形外接圆的方程
依题意可知圆心在 ![]() 轴上,且过原点故可设所求的圆方程为:
轴上,且过原点故可设所求的圆方程为:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 所求的圆方程为
所求的圆方程为
![]()
例2 顶点在原点,焦点在
![]() 轴上的抛物线截直线
轴上的抛物线截直线 ![]() 所得的弦长
所得的弦长 ![]() ,求此抛物线方程.
,求此抛物线方程.
解:设所求的抛物线方程为 ![]() ,
, ![]() ,
, ![]() ,
,
把直线 ![]() 代入
代入 ![]() 得
得 ![]() ,
,
由 ![]() 得
得 ![]() 或
或 ![]() ,
,
又 ![]() ,
,
![]()
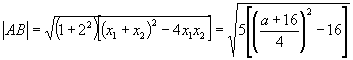
![]()
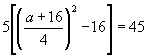
![]()
![]() 或
或 ![]()
故所求的抛物线方程为 ![]() 或
或 ![]()
点评:顶点在原点、焦点在 ![]() 轴上的抛物线有开口向左向右两种情形,因此,方程设为
轴上的抛物线有开口向左向右两种情形,因此,方程设为 ![]() ,这样就避免讨论,简化解题过程.
,这样就避免讨论,简化解题过程.
例3 定长为3的线段 ![]() 的端点
的端点 ![]() 在抛物线
在抛物线 ![]() 上移动,求
上移动,求 ![]() 中点到
中点到 ![]() 轴距离的最小值,并求出此时
轴距离的最小值,并求出此时 ![]() 中点
中点 ![]() 的坐标.
的坐标.
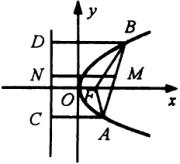 解:如图,设
解:如图,设 ![]() 是抛物线
是抛物线 ![]() 的焦点,
的焦点, ![]() 两点到准线的垂线分别是
两点到准线的垂线分别是 ![]() ,
, ![]() 点到准线的垂线为
点到准线的垂线为 ![]() 为垂足,则:
为垂足,则: ![]()
根据抛物线定义得: ![]()
![]()
设 ![]() 点的横坐标为
点的横坐标为 ![]() ,则:
,则: ![]()
![]()
等号成立的条件是弦 ![]() 过点
过点 ![]() ,
,
由于 ![]()
![]() 过焦点是可能的,此时
过焦点是可能的,此时 ![]() 点到
点到 ![]() 轴最短距离是
轴最短距离是 ![]() ,即
,即 ![]() 的中点横坐标为
的中点横坐标为 ![]() .当
.当 ![]() 在
在![]() 上时,设
上时,设 ![]() 、
、 ![]() 的纵坐标分别为
的纵坐标分别为 ![]() 、
、 ![]() 则
则 ![]() ,从而
,从而 ![]() .
.
![]()
![]() 此时
此时 ![]() 中点的纵坐标为
中点的纵坐标为 ![]()
![]()
![]() 的坐标为
的坐标为 ![]() 时,
时, ![]() 到
到 ![]() 轴距离的最小值为
轴距离的最小值为 ![]() .
.
点评:此题的难点是求最小值.而利用抛物线定义及梯形中位线性质等几何知识使问题变得非常简单,这再一次说明在解题中注意运用圆锥曲线的定义及有关的几何知识,对解题是非常有益的.
例4 (2001年高考题)设抛物线
![]() 的焦点为
的焦点为 ![]() 的直线交抛物线于
的直线交抛物线于 ![]() 、
、 ![]() 两点.点
两点.点 ![]() 在抛物线的准线上,且
在抛物线的准线上,且 ![]() 轴.证明直线
轴.证明直线 ![]() 经过原点
经过原点 ![]() .
.
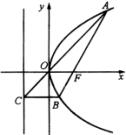 证明一:如图因为抛物线
证明一:如图因为抛物线
![]() 的焦点为
的焦点为 ![]() ,所以经过点
,所以经过点 ![]() 的直线
的直线 ![]() 的方程可设为
的方程可设为 ![]() 代入抛物线方程得
代入抛物线方程得 ![]()
若记 ![]() ,则
,则 ![]() 是该方程的两个根,所以
是该方程的两个根,所以 ![]()
因为 ![]() 轴,且点
轴,且点 ![]() 在准线
在准线 ![]() 上,所以点
上,所以点 ![]() 的坐标为
的坐标为 ![]() ,故直线
,故直线 ![]() 的斜率为
的斜率为 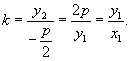
即 ![]() 也是直线
也是直线 ![]() 的斜率,所以直线
的斜率,所以直线 ![]() 经过原点
经过原点 ![]() .
.
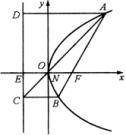 证明二:如图,记
证明二:如图,记
![]() 轴与抛物线准线
轴与抛物线准线 ![]() 的交点为
的交点为 ![]() ,过
,过 ![]() 作
作 ![]() 是垂足,则
是垂足,则 ![]()
连结 ![]() ,与
,与 ![]() 相交于点
相交于点 ![]() ,则
,则 ![]()
根据抛物线的几何性质, ![]()
![]()
即点 ![]() 是
是 ![]() 的中点,与抛物线的顶点
的中点,与抛物线的顶点 ![]() 重合,所以直线
重合,所以直线 ![]() 经过原点
经过原点 ![]() .
.
点评:这是一道几何特浓的解析和何题,它来源于课本习题,就是课本 ![]() 第6题的逆命题.利用平面几何知识来解决解析几何问题简捷、巧妙,应注意体会和应用.
第6题的逆命题.利用平面几何知识来解决解析几何问题简捷、巧妙,应注意体会和应用.
(三)随堂练习
1.证明与抛物线的轴平行的直线和抛物线只有一个交点.
2.从抛物线 ![]() 上各点向
上各点向 ![]() 轴作垂线段,求垂线中点的轨迹方程,并说明它是什么曲线.
轴作垂线段,求垂线中点的轨迹方程,并说明它是什么曲线.
3.设抛物线的顶点为
![]() ,经过焦点垂直于车的直线和抛物线交于两点
,经过焦点垂直于车的直线和抛物线交于两点 ![]() 、
、 ![]() ,经过抛线上一点
,经过抛线上一点
![]() 垂直于车的直线和轴交于点
垂直于车的直线和轴交于点 ![]() ,求证线段
,求证线段 ![]() 是
是 ![]() 和
和 ![]() 的比例中项.
的比例中项.
答案:
1.设抛物线的方程为
![]() ,平行于抛物线的轴的直线的方程为
,平行于抛物线的轴的直线的方程为 ![]() ,由
,由 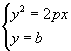 得
得 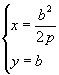
因为方程组只有一个解,所以抛物线 ![]() 与平行于其轴的直线
与平行于其轴的直线 ![]() 只有一个交点.
只有一个交点.
2.设垂线段的中点坐标为
![]() ,抛物上相应点的坐标为
,抛物上相应点的坐标为 ![]() ,根据题意
,根据题意 ![]() 代入
代入 ![]()
由方程可知轨迹是顶点在原点,焦点坐标为 ![]() 的抛物线
的抛物线
3.设抛物线方程为
![]() ,则
,则 ![]() 点的坐标为
点的坐标为 ![]() ,
, ![]() 点的坐标为
点的坐标为 ![]() 设
设 ![]() 点的坐标为
点的坐标为 ![]() ,则
,则 ![]() 点的坐标为
点的坐标为 ![]() .
.
因为 ![]() 所以
所以 ![]()
即 ![]() 是
是 ![]() 与
与 ![]() 的比例中项
的比例中项
(四)总结提炼
1.直线与抛物线的位置关系
设抛物线方程为 ![]() ,当直线斜率存在时,把直线方程代入抛物线方程得关于
,当直线斜率存在时,把直线方程代入抛物线方程得关于 ![]() (或
(或 ![]() )的一元二次方程(二次项系数为
)的一元二次方程(二次项系数为 ![]() )
)
直线与抛物线有两个公共点 
直线与抛物线有一个公共点  ,或二次项系数
,或二次项系数 ![]() (此时直线平行与抛物线的对称轴);
(此时直线平行与抛物线的对称轴);
直线与抛物线没有公共点 
这里特别要注意 ![]() 不是直线和抛物线只有一个公共点的充要条件,当直线平行于抛物线的对称轴时,也只有一个公共点.
不是直线和抛物线只有一个公共点的充要条件,当直线平行于抛物线的对称轴时,也只有一个公共点.
2.要重视抛物线定义的应用,“回归定义”有时使问题变得简捷明确,利用坐标法求曲线的方程并研究其性质,体现解析几何反映的数学思想方法.
(五)布置作业
1.过 ![]() 作直线
作直线 ![]() 与抛物线
与抛物线 ![]() 仅有一个公共点的直线共有( )
仅有一个公共点的直线共有( )
A.3条 B.2条 C.1条 D.不能确定
2.已知抛物线 ![]() 上有一点
上有一点 ![]() ,它到焦点
,它到焦点 ![]() 的距离为5,
的距离为5, ![]() 为原点则
为原点则 ![]() 的面积为( )
的面积为( )
A.1 B. ![]() C.2 D.
C.2 D. ![]()
3.过抛物线 ![]() 的焦点
的焦点 ![]() 作一直线交抛物线于
作一直线交抛物线于 ![]() 、
、 ![]() 两点,若线段
两点,若线段 ![]() 与
与 ![]() 的长分别是
的长分别是 ![]() 、
、 ![]() 则
则 ![]() 等于( )
等于( )
 A.
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
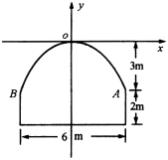
4.某隧道横断面由抛物线及矩形的三边组成,尺寸如图,某卡车空车时能通过此隧道.现载一集装箱,箱宽3米,车与箱共高 ![]() 米,此车能否通过隧道?并说明理由.
米,此车能否通过隧道?并说明理由.
5.过抛物线焦点的一条直线与它交于两点
![]() 、
、 ![]() ,经过点
,经过点 ![]() 和抛物线顶点的直线交准线于点
和抛物线顶点的直线交准线于点 ![]() ,求沿直线
,求沿直线 ![]() 平行于抛物线的对称轴.
平行于抛物线的对称轴.
6.已知抛物线 ![]() 上存在关于直线
上存在关于直线 ![]() 对称的两点,求实数
对称的两点,求实数 ![]() 的取值范围.
的取值范围.
答案:1.A 2.C 3.C
4.取隧道横断面抛物线的顶点为原点,对称轴为
![]() 轴建立直角坐标系.
轴建立直角坐标系.
![]() ,依题意,点
,依题意,点 ![]() 在此抛物线上,代入抛物线方程得
在此抛物线上,代入抛物线方程得
![]() 则
则 ![]()
![]() 抛物线方程为
抛物线方程为 ![]()
又车与箱共高 ![]() 米,则顶部所在直线方程为
米,则顶部所在直线方程为 ![]() . 代入抛物线方程
. 代入抛物线方程 ![]() 即
即 ![]() 米高处隧道的宽为
米高处隧道的宽为 ![]() 米,由于
米,由于 ![]() ,因此这时车不能通过隧道.
,因此这时车不能通过隧道.
5.设抛物线的方程为
![]() ,则焦点
,则焦点 ![]() ,准线
,准线 ![]() ,
,
设 ![]() 的直线方程为
的直线方程为 ![]()
由 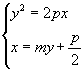 得
得 ![]() .
.
设 ![]() 则
则 ![]() ,
,
直线 ![]() 的方程为
的方程为 ![]() 把
把 ![]() 代入得
代入得 ![]() .
.
![]()
![]() .
.
因为 ![]() 所以直线
所以直线 ![]() 平行于抛物线的对称轴.
平行于抛物线的对称轴.
6.设抛物线上的
![]() 两点关于直线
两点关于直线 ![]() 对称,则
对称,则 ![]() 与
与 ![]() 垂直,可设
垂直,可设 ![]() 的方程为
的方程为 ![]() ,代入
,代入 ![]() ,整理得:
,整理得: ![]()
设 ![]() 、
、 ![]() ,时,
,时, ![]() 即
即 ![]() ①
①
且 ![]()
又线段 ![]() 的中点
的中点 ![]() 在直线
在直线 ![]() 上,则
上,则 ![]() 即
即 ![]() ②
②
把②代入①得 ![]() ∴
∴ ![]()
而 ![]() 故
故 ![]() .
.
(六)板书设计
|
8.6 抛物线的简单几何性(二) |
||
|
一、复习抛物线的几何性 二、例题分析 例1 |
例2 例3 |
例4 三、总结 |