 设为首页
设为首页
 加入收藏
加入收藏
教学设计示例(第一课时)
双曲线及其标准方程
教学目标
掌握双曲线的定义,会推导双曲线的标准方程,能根据条件求简单的双曲线标准方程.
教学教程
【复习提问】
由一位学生口答,教师板书.
问题1:椭圆的第一定义是什么?
问题2:椭圆的标准方程是怎样的?
【新知探索】
1.双曲线的概念
如果把上述定义中的“距离的和”改为“距离的差”,那么点的轨迹会发生什么变化?它的方程是怎样的呢?
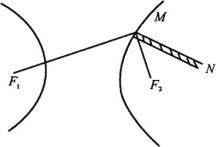 (1)演示
(1)演示
如图,定点 ![]() 、
、 ![]() 是两个按钉,
是两个按钉, ![]() 是一个细套管,点
是一个细套管,点 ![]() 移动时,
移动时, ![]() 是常数,这样就画出双曲线的一支,由
是常数,这样就画出双曲线的一支,由 ![]() 是同一个常数,可以画出双曲线的另一支.
是同一个常数,可以画出双曲线的另一支.
这样作出的曲线就叫做双曲线.
(2)设问
①定点 ![]() 、
、 ![]() 与动点
与动点 ![]() 不在同一平面内,能否得到双曲线?
不在同一平面内,能否得到双曲线?
请学生回答,不能.指出必须“在平面内”.
② ![]() 到
到 ![]() 与
与 ![]() 两点的距离的差有什么关系?
两点的距离的差有什么关系?
请学生回答, ![]() 到
到 ![]() 与
与 ![]() 的距离的差的绝对值相等,否则只表示双曲线的一支,即
的距离的差的绝对值相等,否则只表示双曲线的一支,即 ![]() 是一个常数.
是一个常数.
③这个常是否会大于或等 ![]() ?
?
请学生回答,应小于 ![]() 且大于零.当常数
且大于零.当常数 ![]() 时,轨迹是以
时,轨迹是以 ![]() 、
、 ![]() 为端点的两条射线;当常数
为端点的两条射线;当常数 ![]() 时,无轨迹.
时,无轨迹.
(3)定义
在此基础上,引导学生概括出双曲线的定义:
平面内与两个定点 ![]() 、
、 ![]() 的距离的差的绝对值等于常数(小于
的距离的差的绝对值等于常数(小于 ![]() )的点的轨迹叫做双曲线,这两个定点叫做双曲线的焦点,两焦点的距离叫做双曲线的焦距.
)的点的轨迹叫做双曲线,这两个定点叫做双曲线的焦点,两焦点的距离叫做双曲线的焦距.
2.双曲线的标准方程
现在我们可以用类似求椭圆标准方程的方法来求双曲线的标准方程,请学生思考、回忆椭圆标准方程的推导方法,随即引导学生给出双曲线标准方程的推导.
(1)建系设点
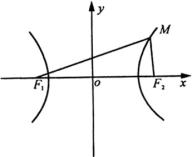 取过焦点
取过焦点 ![]() 、
、 ![]() 的直线为
的直线为 ![]() 轴,线段
轴,线段 ![]() 的垂直平分线为
的垂直平分线为 ![]() 轴建立在直角坐标系(如图).
轴建立在直角坐标系(如图).
设 ![]() 为双曲线上任意一点,双曲线的焦距为
为双曲线上任意一点,双曲线的焦距为 ![]() ,则
,则 ![]() 、
、 ![]() ,又设点
,又设点 ![]() 与
与 ![]() 、
、 ![]() 的距离的差的绝对值等于常数
的距离的差的绝对值等于常数 ![]() .
.
(2)点的焦合
由定义可知,双曲线上点的集合是 ![]()
(3)代数方程
![]()
(4)化简方程
由一位学生演板,教师巡视,
将上述方程化为 ![]()
移项两边平方后整理得: ![]()
两边再平方后整理得: ![]()
由双曲线定义知 ![]() 即
即 ![]() ,∴
,∴ ![]() ,
,
设 ![]() 代入上式整理得:
代入上式整理得: ![]()
这个方程叫做双曲线的标准方程.它所表示的双曲线的焦点在 ![]() 轴上,焦点是
轴上,焦点是 ![]() 、
、 ![]() ,这里
,这里 ![]() .
.
如果双曲线的焦点在 ![]() 轴上,即焦点
轴上,即焦点 ![]() ,
, ![]() ,可以得到方程
,可以得到方程
![]()
这个方程也是双曲线的标准方程.
教师应当指出:
(1)双曲线的标准方程与其定义可联系起来记忆,定义中有“差”,则方程“-”号连接,
(2)双曲线方程中 ![]() ,
, ![]() ,但
,但 ![]() 不一定大于
不一定大于 ![]() ;
;
(3)如果 ![]() 的系数是正的,那么焦点在
的系数是正的,那么焦点在 ![]() 轴上,如果
轴上,如果 ![]() 的系数是正的,那么焦点在
的系数是正的,那么焦点在 ![]() 轴上,有别于椭圆通过比较分母的大小来判定焦点的位置;
轴上,有别于椭圆通过比较分母的大小来判定焦点的位置;
(4)双曲线标准方程中 ![]() 、
、 ![]() 、
、 ![]() 的关系是
的关系是 ![]() ,不同于椭圆方程中
,不同于椭圆方程中 ![]() .
.
【例题分析】
例1 说明:椭圆 ![]() 与双曲线
与双曲线 ![]() 的焦点相同.
的焦点相同.
由一位学生板演完成,答案都是 ![]() .
.
例2 已知两点 ![]() 、
、 ![]() ,求与它们的距离的差的绝对值为6的点的轨迹方程.如果把上面的6改为12,其他条件不变,会出现什么情况?
,求与它们的距离的差的绝对值为6的点的轨迹方程.如果把上面的6改为12,其他条件不变,会出现什么情况?
由教师讲解
解:按定义,所求点的轨迹是以 ![]() 、
、 ![]() 为焦点的双曲线.
为焦点的双曲线.
这里 ![]() ,
, ![]() ,∴
,∴ ![]() 故所求双曲线的方程为
故所求双曲线的方程为
![]()
若 ![]() ,则
,则 ![]() 且
且 ![]() ,所以动点无轨迹.
,所以动点无轨迹.
(三)随堂练习
1.求适合下列条件的双曲线的标准方程.
(1) ![]() ,
, ![]() ;
;
(2)焦点(0,-6),(0,6),经过点(2,-5).
2.已知方程 ![]() ,求它的焦点坐标.
,求它的焦点坐标.
3.已知方程 ![]() 表示双曲线,求
表示双曲线,求 ![]() 的取值范围.
的取值范围.
答案:1.(1) ![]() 或
或 ![]() ;(2)
;(2) ![]() ;2.
;2. 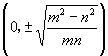 ;3.
;3. ![]() 或
或 ![]()
(四)总结提炼
1.
| 双曲线定义 |
|
|
| 图形 |
|
|
| 标准方程 |
|
|
| 焦点坐标 |
|
|
|
|
|
|
2.双曲线的标准方程可统一写成 ![]() .若
.若 ![]() ,
, ![]() 表示焦点在
表示焦点在 ![]() 轴上的双曲线,若
轴上的双曲线,若 ![]() ,
, ![]() 则表示焦点在
则表示焦点在 ![]() 轴上的双曲线.
轴上的双曲线.
(五)布置作业
1.已知平面上定点 ![]() 、
、 ![]() 及动点
及动点 ![]() ,命题甲:“
,命题甲:“ ![]() (
( ![]() 为常数)”,命题乙:“
为常数)”,命题乙:“ ![]() 点轨迹是
点轨迹是 ![]() 、
、 ![]() 为焦点的双曲线”,则甲是乙的( )
为焦点的双曲线”,则甲是乙的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.已知 ![]() ,
, ![]() ,
, ![]() ,当
,当 ![]() 和5时,
和5时, ![]() 点的轨迹为( )
点的轨迹为( )
A.双曲线和一条直线 B.双曲线和二条射线
C.双曲线一支和一条直线 D.双曲线一支和一条射线
3.双曲线 ![]() 上一点
上一点 ![]() 到它的一个焦点的距离等于1,则点
到它的一个焦点的距离等于1,则点 ![]() 到另一焦点的距离等于___________;若
到另一焦点的距离等于___________;若 ![]() 到它的一个焦点的距离等于17,则点
到它的一个焦点的距离等于17,则点 ![]() 到另一焦点的距离等_____________.
到另一焦点的距离等_____________.
4.如果椭圆 ![]() 与双曲线
与双曲线 ![]() 的焦点相同,那么
的焦点相同,那么 ![]() .
.
5.已知方程 ![]()
(1) ![]() 为何值时方程表示双曲线;
为何值时方程表示双曲线;
(2)证明这些双曲线有共同焦点.
6.已知双曲线的一个焦点坐标为 ![]() ,双曲线上一点
,双曲线上一点 ![]() 到两焦点距离之差的绝对值为24,求双曲线的标准方程.
到两焦点距离之差的绝对值为24,求双曲线的标准方程.
参考答案:
1.B; 2.D; 3.17,1或33; 4.1;
5. ![]() ,当
,当 ![]() 时,方程
时,方程 ![]() 表示双曲线.方程可表示为
表示双曲线.方程可表示为 ![]()
![]() ,焦点坐标为(0,±1).
,焦点坐标为(0,±1).
6. ![]() .
.
(六)板书设计
|
8.3 双曲线及其标准方程(一) |
||
|
(一)复习提问 问题1 问题2 (二)双曲线的概念 1演示 2设问 3定义 |
(三)双曲线的标准方程 1.标准方程的推导 2.说明 |
(四)例题与练习 例1 例2 练习 (五)小结 |
教学设计示例(第二课时)
双曲线及其标准方程
(一)教学目标
1.熟练掌握用待定系数法求双曲线标准方程中的 ![]() ,
, ![]() ,
, ![]() ,并注重用换元法解关于
,并注重用换元法解关于 ![]() 、
、 ![]() 的二元方程组.
的二元方程组.
2.能利用双曲线的有关知识解决与双曲线有关的简单实际应用问题了,了解利用爆炸声的时间差确定爆炸点的准确位置,是双曲线的一个重要应用.
(二)教学过程
【复习提问】
由一位学生口答,教师板书.
问题1.双曲线的定义是什么?问题2.双曲线的标准方程是怎样的?
【新知探索】
双曲线标准方程的求法
由双曲线的定义和标准方程可知,确定双曲线的标准方程需要三个条件,除需指明焦点位置外,还要确定 ![]() 、
、 ![]() 的值.
的值.
【例题分析】
例1 已知双曲线的焦点在
![]() 轴上,并且双曲线上两点
轴上,并且双曲线上两点 ![]() 、
、 ![]() 的坐标分别为
的坐标分别为 ![]() ,
, ![]() ,求双曲线的标准方程.
,求双曲线的标准方程.
分析:这里要用待定系数法,涉及到解方程组,可由教师讲解.
解:因为双曲线的焦点在 ![]() 轴,所以设所求双曲线的标准方程为:
轴,所以设所求双曲线的标准方程为:
![]()
因为 ![]() 、
、 ![]() 在双曲线上,所以点
在双曲线上,所以点 ![]() 、
、 ![]() 的坐标适合方程,将它们的坐标分别代入方程中得到方程组
的坐标适合方程,将它们的坐标分别代入方程中得到方程组 
令 ![]() ,
, ![]() ,则方程组化为:
,则方程组化为: 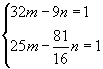
解这个方程组得 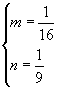
即 ![]() ,
, ![]() ,所以所求双曲线的标准方程为:
,所以所求双曲线的标准方程为: ![]()
教师问:若去掉“焦点在 ![]() 轴上”这一条件,所求的双曲线方程为
轴上”这一条件,所求的双曲线方程为 ![]() 或
或 ![]() 吗?
吗?
这时肯定会有一部分学生回答是
教师引导学生讨论若焦点在 ![]() 轴上的情形.
轴上的情形.
若焦点在 ![]() 轴上,设所求双曲线方程为
轴上,设所求双曲线方程为 ![]()
依题意得 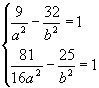 此时无解
此时无解
故所求的双曲线方程仍为 ![]() .
.
教师问:解这道题能不能不讨论呢?
学生回答:能,设所求双曲线方程为 ![]()
依题意得 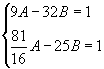 解得
解得 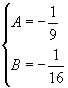
故所求双曲线方程为 ![]() 即
即 ![]() .
.
点评:这样设所求双曲线方程不必讨论且解二元一次方程组简捷迅速,应予掌握.
例2 一炮弹在某处爆炸,在
![]() 处听到爆炸声的时间比在
处听到爆炸声的时间比在 ![]() 处晚
处晚 ![]() ,
,
 (1)爆炸点应在什么样的曲线上?
(1)爆炸点应在什么样的曲线上?
(2)已知 ![]() 、
、 ![]() 两地相距
两地相距 ![]() ,并且此时声速为
,并且此时声速为 ![]() ,求曲线的方程.
,求曲线的方程.
分析:这是一个有关双曲线的应用问题,由教师讲解.
解:(1)由声速及 ![]() 、
、 ![]() 两处听到爆炸声的时间差,可知
两处听到爆炸声的时间差,可知 ![]() 、
、 ![]() 两处与爆炸点的距离的差,因此爆炸点应位于以
两处与爆炸点的距离的差,因此爆炸点应位于以 ![]() 、
、 ![]() 为焦点的双曲线上.
为焦点的双曲线上.
因为爆炸点离 ![]() 处比
处比 ![]() 处更远,所以爆炸点应在靠近
处更远,所以爆炸点应在靠近 ![]() 处的一支上.
处的一支上.
(2)如图,建立直角坐标系,使 ![]() 、
、 ![]() 两点在
两点在 ![]() 轴上,并且原点
轴上,并且原点 ![]() 与线段
与线段 ![]() 的中点重合.
的中点重合.
设爆炸点 ![]() 的坐标为
的坐标为 ![]() ,则:
,则: ![]()
即 ![]() ,∴
,∴ ![]()
又![]() ,即
,即 ![]() ∴
∴ ![]()
![]()
故所求双曲线的方程为 ![]() .
. ![]()
点评:(1)求曲线方程,若没有坐标系,一定要先建立坐标系,按建系设点,列式化简,验证作答的程序进行.
(2)利用两个不同的观测点得同一炮弹爆炸声的时间差,可以确定爆炸点所在的双曲线的方程,但不能确定爆炸点的准确位置,如果再增设一个观测点 ![]() ,利用
,利用 ![]() 、
、 ![]() (或
(或 ![]() 、
、 ![]() )两处测得的爆炸声的时间差,可以求出另一个双曲线的方程,解这两个方程组成的方程组,就能确定爆炸点的准确位置.这是双曲线的一个重要应用.
)两处测得的爆炸声的时间差,可以求出另一个双曲线的方程,解这两个方程组成的方程组,就能确定爆炸点的准确位置.这是双曲线的一个重要应用.
例3 在 ![]() 中,
中, ![]() 固定,顶点
固定,顶点 ![]() 移动.设
移动.设 ![]() ,当三个角有满足条件
,当三个角有满足条件 ![]() 时,求
时,求 ![]() 的轨迹方程.
的轨迹方程.
由一位学生演板,教师订正补充.
解:以 ![]() 所在直线为
所在直线为 ![]() 轴,线段
轴,线段 ![]() 的中点为原点建立直角坐标系,则
的中点为原点建立直角坐标系,则 ![]() 、
、 ![]() 设
设 ![]() 点坐标为
点坐标为 ![]() .
.
由题设: ![]()
根据正弦定理,得: ![]() 即
即 ![]()
可知 ![]() 在以
在以 ![]() 、
、 ![]() 为焦点的双曲线上.
为焦点的双曲线上.
这里 ![]() ∴
∴ ![]() .又
.又 ![]()
∴ ![]()
故所求 ![]() 点的轨迹方程为:
点的轨迹方程为: ![]() .
. ![]()
点评:(1)利用正弦定理实现边角转换再利用双曲线的定义求轨迹是解题的关键.这种满足曲线的定义,可直接写出所求的方程.
(2)求轨迹要做到不重不漏,应把不满足条件的点去掉,这里 ![]() 是
是 ![]() 的顶点,所以应去掉与
的顶点,所以应去掉与 ![]() 、
、 ![]() 共线的点.
共线的点.
(三)随堂练习
1.求焦点在 ![]() 轴上,
轴上, ![]() ,且过点
,且过点 ![]() 的双曲线的标准方程.
的双曲线的标准方程.
2.已知 ![]() 、
、 ![]() 、
、 ![]() ,椭圆过
,椭圆过 ![]() 、
、 ![]() 两点且以
两点且以 ![]() 为其一个焦点,求椭圆另一焦点的轨迹.
为其一个焦点,求椭圆另一焦点的轨迹.
(第1题可在例1后练习,第2题可在例3后练习)
答案:1.设所求双曲线方程为 ![]() ,由题意得
,由题意得 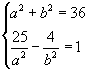 解得
解得  故所求双曲线方程为
故所求双曲线方程为 ![]() .
.
2.设椭圆的另一焦点 ![]() ,由题意得
,由题意得 ![]() ,
,
∴ ![]() .
.
而 ![]() ,
, ![]() 于是
于是 ![]() ,
,
根据双曲线定义可知 ![]() 在以
在以 ![]() 、
、 ![]() 为焦点的双曲线的左支上.
为焦点的双曲线的左支上.
这里 ![]() ,∴
,∴ ![]() ,又
,又 ![]() ∴
∴ ![]() ,
,
故椭圆的另一焦点 ![]() 的轨迹方程为
的轨迹方程为 ![]() .
.
(四)总结提炼
1.求双曲线的标准方程一般应先判定焦点所在的坐标轴,其次再确定 ![]() ,
, ![]() 的值.若已知双曲线经过两个定点,求双曲线方程,设所求双曲线方程为
的值.若已知双曲线经过两个定点,求双曲线方程,设所求双曲线方程为 ![]() 列出关于
列出关于 ![]() 、
、 ![]() 的二元一次方程组.求出
的二元一次方程组.求出 ![]() 、
、 ![]() 既避免了讨论又降低了方程组、未知数的次数,大大减少所需的运算,体现了由繁至简的化归思想.
既避免了讨论又降低了方程组、未知数的次数,大大减少所需的运算,体现了由繁至简的化归思想.
2.求曲线轨迹方程一定要验证,把不满足条件的点、线去掉.
(五)布置作业
1.若点 ![]() 是以
是以 ![]() 、
、 ![]() 为焦点的双曲线
为焦点的双曲线 ![]() 上的一点,则
上的一点,则 ![]() ,且
,且 ![]() ( )
( )
A.2 B.22 C.2或22 D.4或22
2.方程 ![]() 所表示的曲线为
所表示的曲线为 ![]() .
.
①若曲线 ![]() 为椭圆,则
为椭圆,则 ![]() ;②若曲线
;②若曲线 ![]() 为双曲线,则
为双曲线,则 ![]() 或
或 ![]() ;③曲线
;③曲线 ![]() 不可能是圆;④若曲线
不可能是圆;④若曲线 ![]() 表示焦点在
表示焦点在 ![]() 轴上椭圆,则
轴上椭圆,则 ![]()
以上命题正的是( )
A.②③ B.①④ C.②④ D.①②④
3.如果 ![]() 表示焦点在
表示焦点在 ![]() 轴上的双曲线,那么它的半焦距
轴上的双曲线,那么它的半焦距 ![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.(0,2)
C.
B.(0,2)
C. ![]() D.(1,2)
D.(1,2)
4.经过点 ![]() 与
与 ![]() 的双曲线标准方程为_____________.
的双曲线标准方程为_____________.
5.求与圆 ![]() 和圆
和圆 ![]() 都外切的圆的圆心
都外切的圆的圆心 ![]() 的轨迹方程.
的轨迹方程.
6.设声速为 ![]() 米/秒,在相距
米/秒,在相距 ![]() 米的
米的 ![]() 、
、 ![]() 两哨所,听到炮弹爆炸声的时间相差6秒,求炮弹爆炸点的轨迹方程.
两哨所,听到炮弹爆炸声的时间相差6秒,求炮弹爆炸点的轨迹方程.
答案:
1.C; 2.C; 3.A; 4. ![]() ; 5.
; 5. ![]() ;
;
7.以 ![]() 、
、 ![]() 两哨所所在的直线为
两哨所所在的直线为 ![]() 轴,它的中垂线为
轴,它的中垂线为 ![]() 轴建立直角坐标系.得炮弹爆炸点的轨迹方程为
轴建立直角坐标系.得炮弹爆炸点的轨迹方程为 ![]() .
.
(六)板书设计
|
8.3 双曲线及其标准方程(二) |
||
|
(一)复习提问 问题1 问题2 (二)例题分析 例1 |
例2 例3 |
学生练习 三、小结 |