设为首页
加入收藏
当前位置:第十节 解斜三角形应用举例
作者：未知来源：中央电教馆时间：2006/4/8 18:03:15阅读：nyq
字号：小|大
一、教学目标
1．掌握利用正弦定理及余弦定理解任意三角形的方法，会利用解任意三角形的知识解决一些实际问题；
2．能够在解斜三角形应用过程中，灵活地选择正弦定和余弦定理；
3．通过解斜三角形应用举例进一步培养学生将实际问题转化为数学问题，用数学方法解决实际问题的能力；
4．使学生体会知识来源于实际生活，数学知识在实际生活的中的应用，从而培养学生学习数学的兴趣．
二、教学重点 利用解斜三角形解决相关实际问题．
教学难点 利用解斜三角形解决相关实际问题及运算问题．
三、教学具准备
直尺、投影仪．
四、教学过程
例题一
（1）．设置情境
提出问题
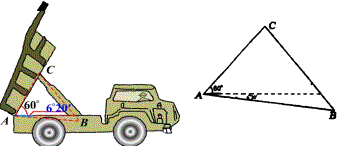如图，自动卸货汽车采用液压机构，设计时需要计算油泵顶杆BC的长度（如图）．已知车厢的最大仰角为60°，油泵顶点B与车厢支点A之间的距离为1.95m，AB与水平线之间的夹角为6°20′，AC长为1.40m，计算BC的长（保留三个有效数字）．
（用多媒体三维动画演示例1的车厢实体模型，也可以用投影仪式挂图）这是一个应用问题，请同学生们想一想，如何计算？
（2）．探索研究
师：什么是最大仰角？
生：最大仰角是车厢立起的最大角度．
建立数学模型
师：例题中涉及一个怎样的三角形？在△ABC中已知什么，要求什么？
生：图中涉及△ABC，在△ABC中已知两边和一角，求BC的长．
师：你能把这一实际问题化归为一道数学题吗？
生：已知△ABC的两边AB＝1.95m，AC＝1.40m，夹角A＝66°20′，求第三边的长．
由学生解答，教师巡视并对学生解答进行讲评小结．
由余弦定理，得
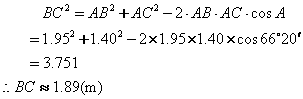
答：顶杆 
约长1.89m。
例题二
（1）．设置情境
提出问题
如下图是曲柄连杆机构的示意图，当曲柄CB绕C点旋转时，通过连杆AB的传递，活塞作直线往复运动，当曲柄在CB位置时，曲柄和连杆成一条直线，连杆的端点A在A处，设连杆AB长为340mm，由柄CB长为85mm，曲柄自CB按顺时针方向旋转80°，求活塞移动的距离（即连杆的端点A移动的距离
）（精确到1mm）
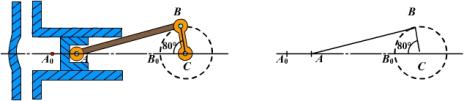
师：用实物模型或多媒体动画演示，让学生观察到B与
重合时，A与 
重合，故 
＝AB＋CB＝425mm，且
＝ 
－AC．
（2）．探索研究建立数学模型
师：通过观察你能建立一个数学模型吗？
生：问题可归结为：已知△ABC中， BC＝85nun，AB＝34mm，∠C＝80°，求AC．
师：如何求AC呢？
生：由已知AB∠C、BC，可先由正弦定理求出∠A，再由三角形内角和为180°求出∠B，最后由正弦定理求出AC．
解：（如图）在△ABC中，由正弦定理可得：
因为BC＜AB，所以A为税角
A＝14°15′
∴ B＝180°－（A＋C）＝85°45′
又由正弦定理：
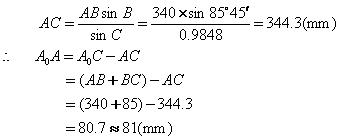
答：活塞移动的距离为81mm．
3．演练反馈（投影）
变式侧题
我舰在敌岛A南偏西50°相距12海里的B处，发现敌舰正由岛沿北偏西10°的方向以10海里/小时的速度航行．问我舰需以多大速度、沿什么方向航行才能用2小时追上敌舰？
师：你能根据方位角画出图吗？
生：（引导启发学生作图）
师：根据题意及画出的方位国请大家建立数学模型．
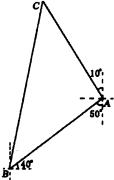生：例题归结为已知三角形的两边和它们的夹角，求第三边及其余角
解：如图，在△ABC中由余弦定理得：
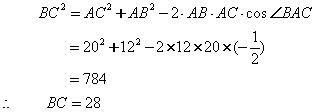
∴我舰的追击速度为14n mile/h
又在△ABC中由正弦定理得：
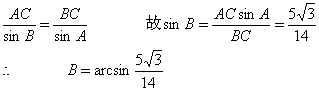
故我舰行的方向为北偏东 
4．总结提炼
（1） 解斜三角形应用题的一般步骤是：
①分析：理解题意，分清已知与未知，画出示意图．
②建模：根据已知条件与求解目标，把已知量与求解量尽量集中在有关的三角形中，建立一个解斜三角形的数学模型．
③求解：利用正弦定理或余弦定理有序地解出三角形，求得数学模型的解．
④检验：检验上述所求的解是否符合实际意义，从而得出实际问题的解．
即解斜三角的基本思路
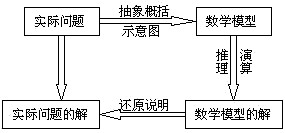
（2）解斜三角形应用题常见的几种情况：
①实际问题经抽象概括后，已知与未知量全部集中在一个三角形中，一次可用正弦定理或余弦定理解之．
②实际问题经抽象概括后，已知量与未知量涉及两个三角形中，这时需按顺序逐步在两个三角形中求出问题的解．
③实际问题经抽象概括后，涉及的三角形只有一个，但由题目已知条件解此三角形需连续使用正弦定理或余弦定理．
五、板书设计
1． 提出问题 2． 分析问题 演示反馈 解决问题 总结提炼 |