 设为首页
设为首页
 加入收藏
加入收藏
教学设计示例(第一课时)
一、教学目标
1.掌握正弦定理及其向量法推导过程;
2.掌握用正弦定理与三角形内角和定理解斜三角形的两类基本问题.
二、教学重点 正弦定理及其推导过程,正弦定理在三角形中的应用;
教学难点 正弦定理的向量法证明以及运用正弦定理解三角形时解的个数的判定.
三、教学准备
直尺、投影仪.
四、教学过程
1.设置情境
师:初中我们已学过解直角三角形,请同学们回忆一下直角三角形的边角关系:
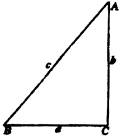 生:Rt
生:Rt![]() 中有
中有![]()
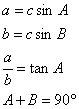
![]()
师:对!利用直角三角形中的这些边角关系对任给直角三角形的两边或一边一角可以求出这个三角形的其他边与其他角.
师:在直角三角形中,你能用其他的边角表示斜边吗?
生:在直角三角形ABC中,![]() 。
。
师:这个式子在任意三角形中也是成立的,这就是我们今天要学的正弦定理(板书正弦定理).
2.探索研究
(1)师:为了证明正弦定理(引导学生复习向量的数量积),![]() ,式子的左边与要证明的式子有相似之处吗?你能否构造一个可以用来证明的式子.
,式子的左边与要证明的式子有相似之处吗?你能否构造一个可以用来证明的式子.
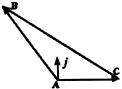
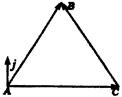 生:如图,在锐角
生:如图,在锐角![]() 中,过A作单位向量j垂直于
中,过A作单位向量j垂直于![]() ,则j与
,则j与![]() 的夹角为
的夹角为![]() 与
与![]() 的夹角为
的夹角为![]() 。
。
由向量的加法可得
![]()
对上面向量等式两边同取与向量j的数量积运算,得到
![]()
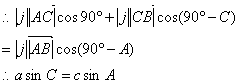
同理,过点C作与![]() 垂直的单位向量j,可得
垂直的单位向量j,可得
![]()
∴![]()
 师:当
师:当![]() 为钝角三角形时,设
为钝角三角形时,设![]() ,如图,过点A作与
,如图,过点A作与![]() 垂直的向量j,则j与
垂直的向量j,则j与![]() 的夹角为
的夹角为![]() ,j与
,j与![]() 的夹角为
的夹角为![]() ,同样可证得
,同样可证得
![]()
师:课后同学考虑一下正弦定理还有没有其它的方法证明?
师:请同学们观察正弦定理,利用正弦定理可以解什么类型的三角形问题?
生:已知两角和任意一边,可以求出其他两边和一角;已知两边和其中一边的对角,可以求出三角形的其他的边和角。
(2)例题分析
例1 在![]() 中,已知
中,已知![]() ,求b(保留两个有效数字)
,求b(保留两个有效数字)
解:∵![]() 且
且![]()
∴![]()
例2 在![]() 中,已知
中,已知![]() ,求
,求![]() 。
。
解:由![]() 得
得![]()
∵![]() 中
中![]() ∴A为锐角
∴
∴A为锐角
∴![]()
例3 在![]() 中,
中,![]() ,求
,求![]() 的面积S。
的面积S。
解:首先可证明:![]() 。
。
这组结论可作公式使用。
其次求b边
![]()
∴由正弦定理,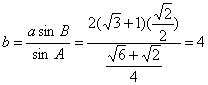
∴![]()
3.演练反馈
(1)在![]() 中,一定成立的等式是(
)
中,一定成立的等式是(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(2)在![]() 中,若
中,若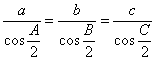 ,则
,则![]() 是( )
是( )
A.等腰三角形 B.等腰直角三角形
C.直角三角形 D.等边三有形
(3)在任一![]() 中,求证
中,求证![]()
参考答案:(1)C;(2)D;(3)证:由于正弦定理:令![]() 代入左边得:左边=
代入左边得:左边=![]()
![]()
![]()
![]()
![]() =右边
=右边
4.总结提炼
(1)三角形常用公式:![]() ;
;![]()
![]()
![]() ;正弦定理以及下节将要学习的余弦定理。
;正弦定理以及下节将要学习的余弦定理。
(2)正弦定理表示形式:![]() (外接圆直径);
(外接圆直径);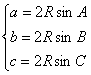 ;
;![]() 。
。
(3)正弦定理应用范围:
①已知两角和任一边,求其他两边及一角。
②已知两边和其中一边对角,求另一边的对角。
③几何作图时,存在多种情况。如已知a、b及A,求作三角形时,要分类讨论,确定解的个数。
五、板书设计
| 课题 1.Rt△中 2.正弦定理及证明 3.例1 2 3 |
4.演练反馈 5.总结提炼 |
教学设计示例(第二课时)
一、教学目标
1.掌握正弦定理在求解三角形中的应用;
2.能够判定利用正弦定理求三角形解情况,灵活运用正弦定理解决实际问题.
二、教学重点 利用正弦定理求解三角形已知两角和一边以及已知两边和其中一边的对角的两种情况.
教学难点 利用正弦定理求解三角形时解的个数的判定.
三、教学具准备
投影仪
四、教学过程
1.设置情境
师:请同学们回想正弦定理的形式,并用文字叙述.
生:在一个三角形中,各边和它所对角的正弦的比相等.即
![]()
师:三角形的基本性质是什么?
生:三角形的三内角和为180°;三角形中大角对大边.
2.探索研究及例题分析
师:利用正弦定理求角时为什么会出现一解、两解、无解的情况呢?下面我们看例题.
例1 在![]() 中,已知
中,已知![]() ,求B(精确到1°)和c边(保留两个有效数字)
,求B(精确到1°)和c边(保留两个有效数字)
师:本题给出的条件是两边和其一边的对角,你能确定解题顺序吗?
生:先由正弦定理求出![]() ,再由正弦定理求出c边.
,再由正弦定理求出c边.
解:![]()
师:![]() 一定是锐角吗?
一定是锐角吗?
生:不一定,因为![]() ,所以在
,所以在![]() 中,
中,![]() 可能是锐角也可能是钝角.
可能是锐角也可能是钝角.
师:本题中因为![]() 或
或![]() 都合题意 ∴有两解
都合题意 ∴有两解
![]() 或
或![]()
我们在解题之前可以先根据大角对大边的性质对已知条件进行分析,判断解的个数,从而优化解题过程.
练习:(投影)
你能根据各已知条件,判定![]() 的解的个数吗?
的解的个数吗?
(1)![]() ,求B;
,求B;
(2)![]() ,求B;
,求B;
(3)![]() ,求B;
,求B;
(4)![]() ,求B.
,求B.
(参考答案:(1)![]() ,B只能是锐角,仅有一解:(2)
,B只能是锐角,仅有一解:(2)![]() ,B只能是锐角,仅有一解;(3)
,B只能是锐角,仅有一解;(3)![]() ,只有一解;(4)有两解.)
,只有一解;(4)有两解.)
例2 在![]() 中,已知
中,已知![]() ,求B(精确到1°)和c(保留两个有效数字).
,求B(精确到1°)和c(保留两个有效数字).
解:已知![]() ,所以
,所以![]() 也是锐角.
也是锐角.
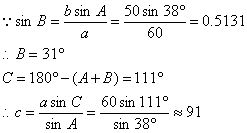
3.演练反馈(投影)
在![]() 中,已知
中,已知![]() ,解这个三角形.(角度精确到1°,边长保留两位有效数字.)
,解这个三角形.(角度精确到1°,边长保留两位有效数字.)
略解:![]() (计算器程序见附1)
(计算器程序见附1)
∴![]()
当![]() 时,
时,![]() ∴
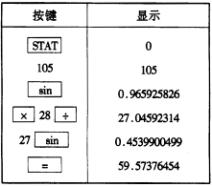
∴![]() (附2)
(附2)
当![]() 时,
时,![]() ∴
∴![]() .
.
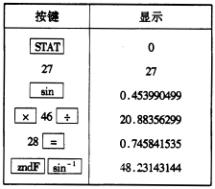
注:在复杂计算中可以使用计算器,本题附1、附2程序如下.
附1
附2
4.总结提炼
(1)![]() 中,因
中,因![]() ,故由
,故由![]() 的值,一般可有两个角、一个角之分,即解不一定惟一.
的值,一般可有两个角、一个角之分,即解不一定惟一.
(2)已知a、b及A作三角形,其解的情况如下:
①A为锐角时
若![]() ,则可用一个三角形如图(1)
,则可用一个三角形如图(1)
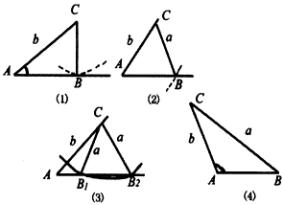
若![]() ,则可作一解,如图(2).
,则可作一解,如图(2).
若![]() ,则可作两解,如图(3).
,则可作两解,如图(3).
②若A为直角或钝角时
若![]() ,则可作一解,如图(4)
,则可作一解,如图(4)
③解三角时可使用计算器.
五、板书设计
|
课题 1.复习 2.例题分析 例1 例2 例3 |
演练反馈 总结提炼 |
教学设计示例(第三课时)
一、教学目标
1.掌握余弦定理的两种表示形式及其推导过程;
2.会用余弦定理解决具体问题;
3.通过余弦定理的向量法证明体会向量工具性.
二、教学重点 余弦定理及其向量法的证明,余弦定理及其变形公式在解三角形中的应用.
教学难点 余弦定理的向量法的证明.
三、教学具准备
直尺,投影仪。
四、教学过程
1.设置情境
师:什么叫做正弦定理,用正弦定理解三角形必须已知哪些量?
生:在一个三角形中,各边和它所对角的正弦的比相等,这就叫做正弦定理.用正弦定理解三角形,必须是已知三角形的两角和一边或者是已知两边和其中一边的对角.
师:在一个三角形中已知两边和这两边的夹角能用正弦定理解这个三角形吗?为什么?
生:不能!因为正弦定理中的任一等号两边都有两个未知量.
师:为了要解这样的三角形,我们今天讲余弦定理.(板书课题----余弦定理)
2.探索研究
(1)我们知道,对于一个直角三角形来说,它的斜边的平方等于两条直角边的平方和,那么对于任意一个三角形来说,是否也可以根据一个角和夹此角的两边,求出此角的对边呢?
师:如图所示,在![]() 中,AB、BC、CA的长分别为c、a、b.由向量加法得:
中,AB、BC、CA的长分别为c、a、b.由向量加法得:
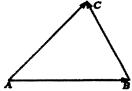
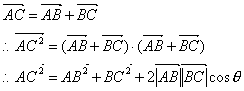
师:![]() 是哪两个向量的夹角呢,它与角B有什么关系?
是哪两个向量的夹角呢,它与角B有什么关系?
生:![]() 是向量
是向量![]() 与向量
与向量![]() 的夹角,它与
的夹角,它与![]() 互补,即
互补,即![]() 。
。
师:由此我们得到
![]()
同理可得
![]()
这就是我要讲的余弦定理,你能用文字叙述吗?
生:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.
师:余弦定理左边有几项?右边有几项?式于中有几个量?
生:左边一个量,右边有三个量,共三边和一个角.
师:余弦定理还可作哪些变形呢?
生:![]()
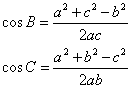
师:利用余弦定理可以解决怎样的三角形问题?
生:①已知三角形三边求角;
②已知两边和它们的夹角,求第三边。
(2)例题分析
例1 在![]() 中,已知
中,已知![]() ,求A、B和C(精确到1°)。
,求A、B和C(精确到1°)。
解:![]()
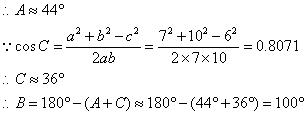
练习(投影)
变式(1):已知条件不变,结论换成判定![]() 的形状。
的形状。
变式(2):已知条件不变,结论换成求![]() 的面积。
的面积。
参考答案:
(1)![]() 的形状由大边b所对角B的范围确定,引导学生得出:
的形状由大边b所对角B的范围确定,引导学生得出:![]() 。
。
(2)先求出一个角,再利用面积公式:![]()
3.演练反馈(投影)
(1)已知![]() 中,
中,![]() ,求B。
,求B。
(2)已知![]() 中,
中,![]() ,求a。
,求a。
(3)已知![]() 中,
中,![]() ,求a并判定三角形的形状。
,求a并判定三角形的形状。
参考答案:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 为等腰三角形。
为等腰三角形。
4.总结提炼
(1)余弦定理适用任何三角形。
(2)余弦定理的作用:已知两边及两边夹角求第三边;已知三边求三角;判断三角形形状。
(3)由余弦定理可知
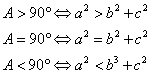
五、板书设计
|
(1)余弦定理 (4)变式训练 (2)余弦定理的使用 (5)演练反馈 (3)例1 (6)总结提炼 |