第七节 平面向量数量积的坐标表示

教学设计示例

一．教学目标

　　1．掌握平面向量数量积的坐标表示和运算，掌握向量垂直的坐标表示的充要条件，掌握平面内两点间的距离公式．

　　（1）根据向量的坐标计算它们的数量积，由数量积的坐标形式求两个向量的夹角．

　　（2）运用向量垂直的坐标表示的充要条件解决有关问题，特别是运用坐标法证明两个向量垂直．

　　（3）根据已知条件灵活运用平面内两点间的距离公式．

　　2．通过本节内容的研究学习，培养学生的动手能力和探索精神．

　　3．通过平面向量数量积的数与形两种表示的相互转化，使学生进一步体会数形结合思想，增强用两种方法——向量法与坐标法处理向量问题的意识．

二．教学重点  平面向量数量积的坐标表示，及向量垂直的坐标表示的充要条件．

　　教学难点  平面向量数量积的两种形式的内在联系及有关知识的灵活运用.

三．教学具准备

　　直尺、投影仪

四．教学过程

　　1．设置情境

　　我们知道，向量的表示形式不同，对其运算的表达方式也会改变．向量的坐标表示，为我们解决向量的加、减、数乘向量带来了极大的方便，那么向量的坐标表示，对数量积的表达方式会带来哪些变化呢？

　　本节课我们就来讨论这一问题

　　2．探索研究

　　（1）师：请同学思考一下，如何用向量的长度、夹角反映数量积？又如何用数量积、长度来反映夹角？向量的运算律有哪些？

　　生： ，

　　运算律有1．

　　2．

　　3．

　　师：已知 ，怎样用 、 的坐标表示 呢？请同学看下列问题（投影）

　　设① ___________  ② ____________

　　　③ ____________   ④ ____________

　　参考答案①1；②1；③0；④0.

　　师：你能推导出 的坐标公式吗？

　　师：

　　　　　　

　　　　　　

　　师：正确！这就是向量的数量积的坐标表示，类似可得：   . 若设 、 则 ，这就是 、 两点间的距离公式.

　　师：请同学写出向量夹角公式的坐标式，向量平行和垂直的坐标表示式.

　　生：（1）

　　　　（2）

　　　　（3）

　　（2）例题分析

　　【例1】设 ， ，求 .

　　解：

　　问： 、 夹角多大？

　　【例2】已知 ， ， ，求证 是直角三角形.

　　证明：∵ 　

　　　　　∴

　　　　　 是直角三角形.

　　问：还有其他证明方法吗？

　　（可计算 、 、 ，然后用勾股定理验证）

　　【例3】求与向量 的夹角为 的单位向量.

　　分析：单位向量其长为1.

　　解：设所求向量为

　　∵ 与 成

　　∴

　　另一方面 

　　∴ ……①

　　又 ……②

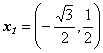　　联立解之： ， 或 ， .

　　∴ 或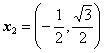

　　说明：也可以设 ，还可以先把 单位化.

　　3．演练反馈（投影）

　　（1）已知 ， 且 ，求 .

　　（2）已知 ，求与 垂直的单位向量.

　　（3） 中， ， ，求 的值.

　　提示：分类讨论

参考答案：

　　（1）

　　（2）∵ ，则易证 或 与 垂直.

　　　　∴ 与 垂直的单位向量为 ，或 ，而 .

　　　　∴ 或 为所求答案.

　　（3）解：① 时，

　　　　　　② 时，

　　　　　　③ 时， .

　　4．总结提炼

　　（1）用坐标表示的数量积公式，常用来计算两向量的夹角.

　　（2）两向量垂直时，在表达方式上有一定技巧，如 与 总是垂直的。

　　（3）把一平面向量单位化，有时能给讨论问题带来方便，比如求 在 方向的投影，不妨先把 单位化，为 ，则 就是所求答案。

五．板书设计

课题 1．复习数量积定义式 2．计算基度向量 、 的数量积3．推导 公式

例题 1 2 3 演练反馈 总结提炼