第三节 实数与向量的积

教学设计示例（第一课时）

一．教学目标

　　1．理解并掌握实数与向量的积的意义．

　　2．理解两个向量共线的充要条件，能根据条件判断两个向量是否共线；

　　3．通过对实数与向量的积的学习培养学生的观察、分析、归纳、抽象的思维能力，了解事物运动变化的辩证思想.

二．教学重点：实数与向量的积的定义、运算律，向量共线的充要条件；

　　教学难点：理解实数与向量的积的定义，向量共线的充要条件；

三．教学具准备

　　直尺、投影仪．

四．教学过程

　　1．设置情境

　　我们知道，位移、力、速度、加速度等都是向量，而时间、质量等都是数量，这些向量与数量的关系常常在物理公式中体现，如力与加速度的关系f=ma，位移与速度的关系s=vt．这些公式都是实数与向量间的关系．

　　师：我们已经学习了向量的加法，请同学们作出 和 向量，（已知向量已作在投影片上），并请同学们指出相加后，和的长度与方向有什么变化？这些变化与哪些因素有关？

　　生： 的长度是 的长度的3倍，其方向与 的方向相同， 的长度是 长度的3倍，其方向与 的方向相反．

　　师：很好！本节课我们就来讨论实数与向量的乘积问题，（板书课题：实数与向量的乘积（一））

　　2．探索研究

　　师：请大家根据上述问题并作一下类比，看看怎样定义实数与向量的积？可结合教材思考．

　　生：我想这样规定：实数 与向量 的积就是 ，它还是一个向量．

　　师：想法很好．不过我们要对实数 与向量 相乘的含义作一番解释才行．

　　实数 与向量 的积是一个向量，记作 ，它的长度和方向规定如下：

　　（1）

　　（2） 时， 的方向与 的方向相同；当 时， 的方向与 的方向相反；特别地，当 或 时，

　　下面我们讨论作为数乘向量的基本运算律：

　　师：求作向量 和 （ 为非零向量）并进行比较，向量 与向量 相等吗？（引导学生从模的大小与方向两个方面进行比较）

　　生： ，

　　师：设 、 为任意向量， ， 为任意实数，则有：

　　（1） 　　（2） 　（3）

　　通常将（1）称为结合律，（2）（3）称为分配律，有时为了区别，也把（2）叫第一分配律，（3）叫第二分配律．

　　请看例题

　　【例1】计算：（1） ， （2） ．

　　（3）

　　解：（1）原式

　　（2）原式

　　（3）原式 ．

　　下面我们研究共线向量与实乘向量的关系．

　　师：请同学们观察 ， ，有什么关系．

　　生：因为 ，所以 、 是共线向量．

　　师：若 、 是共线向量，能否得出 ？为什么，可得出 吗？为什么？

　　生：可以！因为 、 共线，它们的方向相同或相反．

　　师：由此可得向量共线的充要条件．向量 与非零向量 共线的充分必要条件是有且仅有一个实数 ，使得

　　此即教材中的定理．

　　对此定理的证明，是两层来说明的．

　　其一，若存在实数 ，使 ，则由实数与向量乘积定义中的第（2）条知 与 共线，即 与 共线．

　　其二，若 与 共线，且不妨令 ，设 （这是实数概念）．接下来看 、 方向如何：① 、 同向，则 ，②若 、 反向，则记 ，总而言之，存在实数 （ 或 ）使 ．

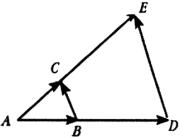　　【例2】如图：已知 ， ，试判断 与 是否共线．

　　解：∵

　　∴ 与 共线．

练习（投影仪）

　　设 、 是两个不共线向量，已 ， ，若 、 、 三点共线，求 的值．

参考答案

　　∵ 、 、 三点共线．

　　∴ 、 共线 存在实数 ，使

　　即

　　∴ ，

3．练习反馈（投影仪）

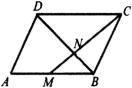
　　（1）若 为 的对角线交点， ， ，则 等于（     ）

　　A．          B．          C．            D．

　　（2）在△ 中，点 、 、 分别是边 、 、 的中点，那么 ．

　　（3）如图所示，在平行四边形 中， 是 中点，点 是 上一点， 求证 、 、 三点共线．

参考答案：

　　（1）B； （2） ；

　　（3）设 ， 则 又 ，∴ ∴ 、 、 共线．

4．总结提炼

　　（1） 与 的积还是向量， 与 是共线的．

　　（2）一维空间向量的基本定理的内容和证明思路，也是应用该定理解决问题的思路．该定理主要用于证明点共线、求系数、证直线平行等题型问题．

　　（3）运算律暗示我们，化简向量代数式就像计算多项式一样去合并同类项．

五．板书设计

1．实数与向量的积定义 2．运算律 ① ② ③ 3．向量共线定理

例1 2 演练反馈 总结提炼

教学设计示例（第二课时）

一．教学目标

　　1．了解平面向量基本定理的证明．掌握平面向量基本定理及其应用；

　　2．能够在解题中适当地选择基底，使其它向量能够用选取的基底表示．

二．教学重点：平面向量基本定理

　　教学难点：理解平面向量基本定理．

三．教学具准备

　　直尺、投影仪．

四．教学过程

　　1．设置情境

　　上节课我们学习了共线向量的基本定理，通过它们判定两个向量是否平行，而且共线向量可由该集合中的任一非零向量表示出来．这个非零向量叫基向量．那么平面上的任一向量是否也具有类似属性呢？如果是这样的话，对平面上任一向量的研究就可以化归为对基向量的研究了．

　　2．探索研究

　　师：向量 与非零向量 共线的充要条件是什么？

　　生：有且仅有一个实数 ，使得

　　师：如何作出向量 ？

　　生：在平面上任取一点 ，作 ， ，则

　　师：对！我们知道向量 是向量 与 的合成， 、 也可以看做是由向量 的分解，是不是每一个向量都可以分解两个不共线的向量呢？

　　平面向量基本定理：如果 、 是同一平面内的两个不共线向量，那么对这一平面内的任一向量 ，有且只有一对实数 ， 使

　　我们把不共线的向量 、 叫做表示这一平面内所有向量的一组基底．

　　说明：①实数 ， 的确定是由平面几何作图得到的，同时也应用了上节课的共线向量基本定理．

　　②对该定理重在使用．

　　下面看例题

　　【例1】已知向量 、 ，求作 ．

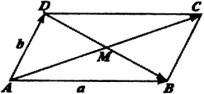　　 【例2】如图所示， 的两条对角线相交于点 ，且 ， ，用 、 表示 、 、 和 ？

　　解：在 中

　　∵

　　　

　　∴

　　　

　　　

　　　

　　说明：①这些表示方法很常用，要熟记

　　②用向量法讨论几何问题，关键是选取适当的基向量表示其他向量，本题的基底就是 、 ，由它可以“生”成 ， ，……．

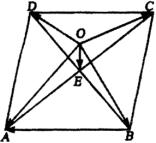【例3】如图所示，已知 的两条对角线 与 交于 ， 是任意一点，求证

　　证明：∵ 是对角线 和 的交点

　　∴ ， ．在△ 中，

　　同理：

　　　　　

　　　　　

　　相加可得：

　　注：本题也可以取基本向量 ， ， ， ，利用三角形中线公式（向量），得 两种表示方式：

　　①

　　②

　　①＋②得 证毕．

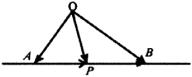　　 【例4】如图所示 、 不共线， （ ），用 ， 表示 ．

　　解   ∵

　　∴

　　　　　

　　　　　

　　　　　

　　　　　

　　说明：①本题是个重要题型：设 为平面上任一点．

　　则： 、 、 三点共线

　　或令 ， 则 、 、 三点共线 （其中 ）

　　②当 时， 常称为△ 的中线公式（向量式）．

3．演练反馈

　　（1）命题 ：向量 与 共线；命题 ：有且只有一个实数 ，使 ；则 是 的（      ）

　　A．充分不必要条件               B．必要不充分条件

　　C．充要条件                     D．不充分不必要条件

　　（2）已知 和 不共线，若 与 共线，则实数 的值等于____________．

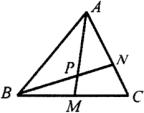
　　（3）如图△ 中，点 是 的中点，点 在边 上，且 ， 与 相交于点 ，求 的值．

参考答案：

　　（1）B　　（2）

　　 （3）解：（如图）设 ， ，则 ，

，∵ 、 、 和 、 、 分别共线，∴存在 、 ，使 ， ．

故 ，而 ．

∴由基本定理得 ∴ ∴ ，即

4．总结提炼

　　（1）当平面内取定一组基底 ， 后，任一向量 都被 、 惟一确定，其含义是存在惟一这数对 ，使 ，则必有 且 ．

　　（2）三点 、 、 共线 （其中 且 ）

五．板书设计