第二节 向量的加法与减法

教学设计示例（第一课时）

一．教学目标

　　（1）掌握向量的加法的定义，会用向量加法的三角形法则和会用向量加法的平行四边形法则作两个向量的和向量；

　　（2）掌握向量加法的交换律和结合律，并会用它们进行计算；

　　（3）启发学生能够发现问题和提出问题，善于独立思考，学会分析问题和创造地解决问题；

　　（4）培养学生化归的数学思想．

二．教学重点：向量的加法的定义，向量加法的三角形法则和平行四边形法则，作两个向量的和向量；

　　教学难点：对向量加法定义的理解．

三．教具：多媒体、实物投影仪

四．教学过程

　　1．设置情境

　　请同学看这样一个问题：（投影）

　　（1）由于大陆和台湾没有直航，因此2003年春节探亲，要先从台北到香港，再从香港到上海，这两次位移之和时什么？

　　（2）如图（2），飞机从 到 ，再改变方向从 到 ，则两次位移的和是 ，应该是_____________．

　　（3）如图（3），船的速度是 ，水流速度是 则两个速度的和是 应该是___________．

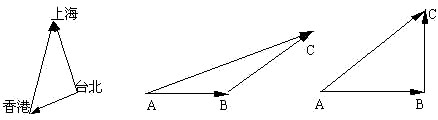
　　生：（1）这人两次的位移的和是从台北到上海；（2）飞机两次位移的和是 ；（3）两个速度的和是 ．

　　师：很好！两人向量的和仍是一个向量．本节课就来研究两个向量的和（板书课题：向量的加法）．

　　2．探索研究

　　（1）向量的加法的定义：

　　已知向量 ，在平面内任取一点A，作 ，则向量 叫做向量 的和。记作： 即

　　零向量与任意向量 ，有

　　（2）两个向量的和向量的作法：

　　①三角形法则:两个向量“首尾”相接

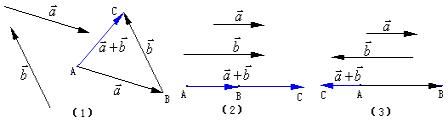
　　注意：1°三角形法则对于两个向量共线时也适用；

　　　　　2°两个向量的和向量仍是一个向量

　　例1．已知向量 ，求作　向量

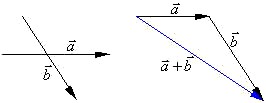
　　作法：在平面内任取一点O，作 ，则

　　②平行四边形法则：

　　由同一点A为起点的两个已知向量 为邻边作平行四边形BCD，则以A为起点的向量 就是向量 的和。这种作两个向量和的方法叫做平行四边形法则

　　注意：平行四边形法则对于两个向量共线时不适用

　　3．向量和与数量和的区别：

　　①当向量 不共线时， 的方向与 不同向，且

　　②当向量 同向时， 的方向与 同向，且

　　　当向量 反向时，若 ，则 的方向与 同向，且 ；若 ，则 的方向与 反向，且 ；4．向量的运算律：

　　①交换律：

　　证明：当向量 不共线时,如上图，作平行四边形ABCD，使 ，

　　则 ,

　　因为 ，

　　所以

　　当向量 共线时，若 与 同向，由向量加法的定义知：

　　 与 同向，且

　　 与 同向，且 ，所以

　　若 与 反向，不妨设 ，同样由向量加法的定义知：

　　 与 同向，且

　　 与 同向，且 ，所以

　　综上，

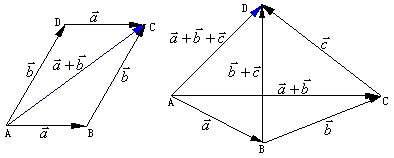
　　②结合律：

　　学生自己验证。

　　由于向量的加法满足交换律和结合律，对于多个向量的加法运算就可以按照任意的次序与任意的组合来进行了

　　例如：

　　　　　

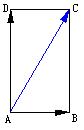　　例2．如图，一艘船从A点出发以 的速度向垂直于对岸的方向行驶，同时喝水的流速为 ，求船实际航行的速度的大小与方向。

　　解：设 表示船垂直于对岸的速度， 表示水流的速度，以AD,AB为邻边作平行四边形ABCD，则 就是船实际航行的速度

　　在 中， ，

　　所以

　　因为

　　答：船实际航行的速度的大小为 ，方向与水流速间的夹角为

4．演练反馈（投影）

　　（1）在平行四边形 中， ， 则用 、 表示向量 的是（     ）

　　A． ＋          B．           C．0          D． ＋

　　（2）若 为△ 内一点， ，则 是△ 的（     ）

　　A．内心           B．外心        C．垂心          D．重心

　　（3）下列各等式或不等式中一定不能成立的个数（     ）

　　① 　　②

　　③ 　　④

　　A．0          B．1          C．2            D．3

5．总结提炼

　　（1） 是一个向量，在三角形法则下：平移 向量，使 的起点与 的终点重合，则 就是以 的起点为起点， 的终点为终点的新向量．

　　（2）一组首尾相接的向量和： ，如图．

　　（3）对任意两个向量 、 ，任有 成立．

五．板书设计

 

1．引例揭示课题 2．例1    例2

演练反馈 总结提炼

教学设计示例（第二课时）

一．教学目标

　　1．明确相反向量的意义，掌握向量的减法，会作两个向量的差向量；

　　2．能利用向量减法的运算法则解决有关问题；

　　3．启发学生能够发现问题和提出问题，善于独立思考，学会分析问题和创造地解决问题；

　　4．过阐述向量的减法运算可以转化为向量加法运算及多个向量的加法运算可以转化成两个向量的加法运算，可以渗透化归的数学思想，使学生理解事物之间相互转化，相互联系的辨证思想，同时由于向量的运算能反映出一些物理规律，从而加强了数学学科与物理学科之间的联系，提高学生的应用意识．

二．教学重点：向量的减法的定义，作两个向量的差向量；

　　教学难点：对向量减法定义的理解．

三．教    具：多媒体、实物投影仪

四．教学过程

　　1．设置情境

　　上节课，我们定义了向量的加法概念，并给出了求作和向量的两种方法．本节课，我们继续学习向量加法的逆运算：减法（板书课题：向量的减法）

　　2．探索研究

　　（1）向量减法

　　①相反向量：与 长度相等，方向相反的向量叫做相反向量。记作

　　规定：零向量的相反向量仍是零向量

　　注意：1° 与 互为相反向量。即

　　　　　2°任意向量与它的相反向量的和是零向量。即

　　　　　3°如果 、 是互为相反向量，那么

　　② 与 的差：向量 加上 的相反向量，叫做 与 的差

即

　　③向量的减法：求两个向量的差的运算叫做向量的减法

　　④ 的作法：已知向量 、 ，在平面内任取一点O，作 ，则 。即 可以表示为从向量 的终点指向向量 的终点的向量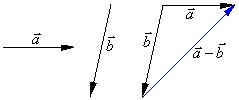

　　⑤思考：为从向量 的终点指向向量 的终点的向量是什么？（ ）

　　师：还可以从加法的逆运算来定义，如下图所示，因为 ，所以 就是 ，因而只要作出了 ，也就作出了 ．

　　要作出 ，可以在平面内任取一点 ，作 ， ，则 ．

　　师：若两向量平行，如何作它们的差向量？两个向量的差仍是一个向量吗？它们的大小如何（ 的几何意义）？方向怎样？

　　生：两个向量的差还是一个向量， 的大小是 ，是连接 、 的终点的线段，方向指向被减向量．

练习：（投影）

　　判断下列命题的真假

　　（1） ．（     ）

　　（2）相反向量就是方向相反的向量．（      ）

　　（3） （     ）

　　（4） （     ）

参考答案：√、×、×、×

　　（2）例题分析

　　【例1】已知向量 、 、 、 ，求作向量 ，

　　师：已知的四个向量的起点不同，要作向量 与 ，首先要做什么？

　　生：首先在平面内任取一点 ，作 ， ， ，

　　作 、 ，则 ，

　

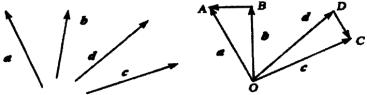
　　【例2】如图所示， 中 ， ，用 、 表示向量 、 ．

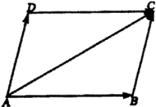师：由平行四边形法则得

　　由作向量差的方法

　　得

练习：（投影）

　　对例2进行变式训练

　　变式一，本例中，当 、 满足什么条件时， 与 互相垂直？

　　变式二，本例中，当 、 满足什么条件时， ？

　　变式三，本例中， 与 有可能相等吗？为什么？

参考答案：

　　变式一：当 为菱形时，即 时， 与 垂直．

　　变式二：当 为长方形时 ，即 ．

　　变式三：不可能，因为 的对角线总是方向不同的．

3．演练反馈（投影）

　　（1）△ 中， ， ，则 等于（     ）

　　A．         B．          C．        D．

　　（2）下列等式中，正确的个数是（      ）

　　① ；  ② ；  ③ ；  ④ ；  ⑤ ．

　　A．5        B．4        C．3         D．2

　　（3）已知 ， ，则 的取值范围是_____________．

参考答案：（1）B；   （2）B；  （3）［3，13］

4．总结提炼

　　（1）相反向量是定义向量减法的基础，减去一个向量等于加上这个向量的相反向量：

　　（2）向量减法有两种定义：①将减法运算转化为加法运算： ②将减法运算定义为加法运算的逆运算：如果 ，则 ．从作图上看这两种定义没有本质区别，前一个定义就是教材采用的定义法，但作图稍繁一点；后一种定义便于作图和记忆，两个有相同起点的向量相减，所得向量是连接两向量终点，并且指向被减向量的终点．

五．板书设计

向量的减法 相反向量              例1．           例2． 向量的减法