第十节 正切函数的图象和性质

4.10 正切函数的图象和性质

第一课时

（一）教学具准备

　　直尺、投影仪．

（二）教学目标

　　1．会用“正切线”和“单移法”作函数 的简图．

　　2．掌握正切函数的性质及其应用．

（三）教学过程

1．设置情境

　　正切函数是区别于正弦函数的又一三角函数，它与正弦函数的最大区别是定义域的不连续性，为了更好研究其性质，我们首先讨论 的作图．

2．探索研究

　　师：请同学们回忆一下，我们是怎样利用单位圆中的正弦线作出 图像的．

　　生：在单位圆上取终边为 （弧度）的角，作出其正弦线 ，设 ，在直角坐标系下作点 ，则点 即为 图像上一点．

　　师：这位同学讲得非常好，本节课我们也将利用单位圆中的正切线来绘制 图像．

　　（1）用正切线作正切函数图像

　　师：首先我们分析一下正切函数 是否为周期函数？

　　生：∵

　　　　∴ 是周期函数， 是它的一个周期．

　　师：对，我们还可以证明， 是它的最小正周期．类似正弦曲线的作法，我们先作正切函数在一个周期上的图像，下面我们利用正切线画出函数 ， 的图像．

　　作法如下：①作直角坐标系，并在直角坐标系 轴左侧作单位圆．

　　　　　　　②把单位圆右半圆分成8等份，分别在单位圆中作出正切线．

　　　　　　　③找横坐标（把 轴上 到 这一段分成8等份）．

　　　　　　　④找纵坐标，正切线平移．

　　　　　　　⑤连线．

　

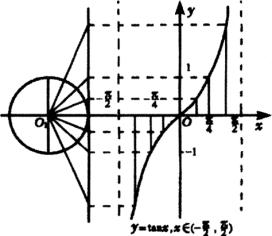
图1

　　根据正切函数的周期性，我们可以把上述图像向左、右扩展，得到正切函数 ， 且 （ ）的图像，并把它叫做正切曲线（如图1）．

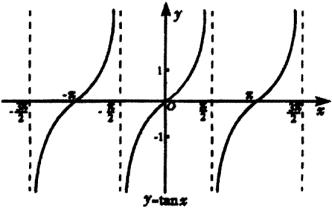
图2

　　（2）正切函数的性质

　　请同学们结合正切函数图像研究正切函数的性质：定义域、值域、周期性、奇偶性和单调性．

　　①定义域：

　　②值域

　　由正切曲线可以看出，当 小于 （ ）且无限亲近于 时， 无限增大，即可以比任意给定的正数大，我们把这种情况记作 （读作 趋向于正无穷大）；当 大于 且无限接近于 ， 无限减小，即取负值且它的绝对值可以比任意给定的正数大，我们把这种情况记作 （读作 趋向于负无穷大）．这就是说， 可以取任何实数值，但没有最大值、最小值．

　　因此，正切函数的值域是实数集 ．

　　③周期性

　　正切函数是周期函数，周期是 ．

　　④奇偶性

　　∵ ，∴正切函数是奇函数，正切曲线关于原点 对称．

　　⑤单调性

　　由正切曲线图像可知：正切函数在开区间（ ， ）， 内都是增函数．

　　（3）例题分析

　　【例1】求函数 的定义域．

　　解：令 ，那么函数 的定义域是

　　由    ，可得  

　　所以函数 的定义域是

　　【例2】不通过求值，比较下列各组中两个正切函数值的大小：

　　（1） 与 ；

　　（2） 与 ．

　　解：（1）∵

　　又  ∵ ，在 上是增函数

　　∴

　　（2）∵

　　　　　

　　又   ∵ ，函数 ， 是增函数，

　　∴   即 ．

　　说明：比较两个正切型实数的大小，关键是把相应的角诱导到 的同一单调区间内，利用 的单调递增性来解决．

　　3．演练反馈（投影）

　　（1）直线 （ 为常数）与正切曲线 （ 为常数且 ）相交的相邻两点间的距离是（      ）

　　A．　　B．　　C．　　D．与 值有关

　　（2） 是 的（       ）

　　A．充分不必要条件　　B．必要不充分条件

　　C．充要条件　　　　　D．既不充分也不必要条件

　　（3）根据三角函数的图像写出下列不等式成立的角 集合

　　①　　②

参考答案：

　　（1）C．注： 与 相邻两点之间距离即为周期长

　　（2）D．注：由 ，但 ，反之 ，但

　　（3）①

　　　　　②

　　4．总结提炼

　　（1） 的作图是利用平移正切线得到的，当我们获得 上图像后，再利用周期性把该段图像向左右延伸、平移。

　　（2） 性质．

定义域	值域	周期	奇偶性	单调增区间	对称中心	渐近线方程
			奇函数			，

（四）板书设计

课题…… 1．用正切线作正切函数图像 2．正切函数的性质

例1 例2 演练反馈

总结提炼

4.10 正切函数的图象和性质

第二课时

（一）教学具准备

　　投影仪

（二）教学目标

　　运用正切函数图像及性质解决问题．

（三）教学过程

　　1．设置情境

　　本节课，我们将综合应用正切函数的性质，讨论泛正切函数的性质．

　　2．探索研究

　　（1）复习引入

　　师：上节课我们学习了正切函数的作图及性质，下面请同学们复述一下正切函数 的主要性质

　　生：正切函数 ，定义域为 ；值域为 ；周期为 ；单调递增区间 ， ．

　　（2）例题分析

　　【例1】判断下列函数的奇偶性：

　　（1） ；　　（2） ；

　　分析：根据函数的奇偶性定义及负角的诱导公式进行判断．

　　解：（1）∵ 的定义域为 关于原点对称．

　　

　　∴ 为偶函数

　　（2）∵ 的定义域为 关于原点对称，且 且 ，

　　∴ 即不是奇函数又不是偶函数．

　　说明：函数具有奇、偶性的必要条件之一是定义域关于原点对称，故难证 或 成立之前，要先判断定义域是否关于原点对称．

　　【例2】求下列函数的单调区间：

　　（1） ；　　（2） ．

　　分析：利用复合函数的单调性求解．

　　解：（1）令 ，则

　　∵ 为增函数， 在 ， 上单调递增，

　　∴ 在 ，即 上单调递增．

　　（2）令 ，则

　　∵ 为减函数， 在 上单调递增，

　　∴ 在 上单调递减，即 在 上单调递减．

　　【例3】求下列函数的周期：

　　（1） 　　（2） ．

　　分析：利用周期函数定义及正切函数最小正周期为 来解．

　　解：（1）

　　　　　　　　　

　　　　　　　　　

　　　　　　　　　

　　∴周期

　　（2）

　　　　　　　

　　　　　　　

　　　　　　　

　　∴周期

　　师：从上面两例，你能得到函数 的周期吗？

　　生：周期

　　【例4】有两个函数 ， （其中 ），已知它们的周期之和为 ，且 ， ，求 、 、 的值．

　　解：∵ 的周期为 ， 的周期为 ，由已知 得

　　∴函数式为 ， ，由已知，得方程组

　　

　　即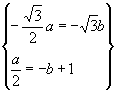 解得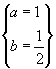

　　∴ ， ，

　　［参考例题］求函数 的定义域．

　　解：所求自变量 必须满足

　　        （ ）

　　                 （ ）

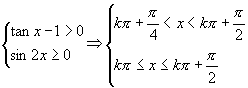　　故其定义域为

　　3．演练反馈（投影）

　　（1）下列函数中，同时满足①在 上递增；②以 为周期；③是奇函数的是（      ）

　　A．　　B．　　C．　　D．

　　（2）作出函数    ，且 的简图．

　　（3）函数 的图像被平行直线_______隔开，与 轴交点的横坐标是__________，与 轴交点的纵坐标是_________，周期________，定义域__________，它的奇偶性是_____________．

参考答案：（1）C．

　（2）

如图

　　

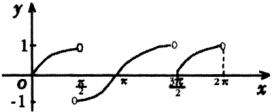
　　（3） （ ）； ，（ ）；1； ； ；非奇非偶函数．

　　4．总结提炼

　　（1） 的周期公式 ，它没有极值，正切函数在定义域上不具有单调性（非增函数），了不存在减区间．

　　（2）求复合函数 的单调区间，应首先把 、 变换为正值，再用复合函数的单调性判断法则求解．

（四）板书设计

课题—— 例1 例2 例3 例4

［参考例题］ 演练反馈 总结提炼