 设为首页
设为首页
 加入收藏
加入收藏
教学设计示例
4.9 函数![]() 的图像
的图像
第一课时
(一)教学具准备
直尺、投影仪.
(二)教学目标
掌握由![]()
(三)教学过程
1.设置情境
函数![]() (
(![]() 、
、![]() 、
、![]() 是常数)广泛应用于物理和工程技术上、例如,物体作简谐振动时,位移
是常数)广泛应用于物理和工程技术上、例如,物体作简谐振动时,位移![]() 与时间
与时间![]() 的关系,交流电中电流强度
的关系,交流电中电流强度![]() 与时间
与时间![]() 的关系等,都可用这类函数来表示.我们知道,图像是函数的最直观的模型,如何作出这类函数的图像呢?下面我们先从函数
的关系等,都可用这类函数来表示.我们知道,图像是函数的最直观的模型,如何作出这类函数的图像呢?下面我们先从函数![]() 与
与![]() 的简图的作法学起.(板书课题)—函数
的简图的作法学起.(板书课题)—函数![]() 与
与![]() 的图像.
的图像.
2.探索研究
(可借助多媒体)
(1)函数![]() 与
与![]() 的图像的联系
的图像的联系
【例1】画出函数![]() 及
及![]() (
(![]() )的简图.
)的简图.
解:函数![]() 及
及![]() 的周期均为
的周期均为![]() ,我们先作
,我们先作![]() 上的简图.
上的简图.
列表并描点作图(图1)
|
|
0 |
|
|
|
|
|
|
0 |
1 |
0 |
-1 |
0 |
|
|
0 |
2 |
0 |
-2 |
0 |
|
|
0 |
|
0 |
|
0 |
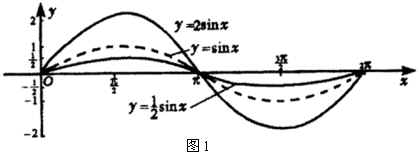
利用这两个函数的周期性,我们可以把它们在![]() 上的简图向左、右分别扩展,从而得到它们的简图.
上的简图向左、右分别扩展,从而得到它们的简图.
![]() 的图像与
的图像与![]() 的图像之间有何联系?请一位同学说出
的图像之间有何联系?请一位同学说出![]() 的值域和最值.
的值域和最值.
生:![]() 的图像可以看做是把
的图像可以看做是把![]() 的图像上所有点的纵坐标伸长到原来的2倍(横坐标不变)而得到的.
的图像上所有点的纵坐标伸长到原来的2倍(横坐标不变)而得到的.![]() ,
,![]() 的值域是
的值域是![]() ,最大值是2,最小值是-2.
,最大值是2,最小值是-2.
师:![]() 的图像与
的图像与![]() 的图像有何联系?并请你说出
的图像有何联系?并请你说出![]() 的值域和最值.
的值域和最值.
生:![]() 的图像可以看做是把
的图像可以看做是把![]() 的图像上所有点的纵坐标缩短到原来的
的图像上所有点的纵坐标缩短到原来的![]() 倍,(横坐标不变)而得到的,
倍,(横坐标不变)而得到的,![]() ,
,![]() 的值域是
的值域是![]() ,最大值是
,最大值是![]() ,最小值是
,最小值是![]() .
.
师:由例1中![]() 、
、![]() 与
与![]() 的图像的联系,我们来探求函数
的图像的联系,我们来探求函数![]() (
(![]() 且
且![]() )的图像与
)的图像与![]() 的图像之间的联系.
的图像之间的联系.
函数![]() (
(![]() 且
且![]() )的图像可以看做是把
)的图像可以看做是把![]() 的图像上所有点的纵坐标伸长(当
的图像上所有点的纵坐标伸长(当![]() 时)或缩短(当
时)或缩短(当![]() )到原来的
)到原来的![]() 倍(横坐标不变)而得到,这种变换称为振幅变换,它是由
倍(横坐标不变)而得到,这种变换称为振幅变换,它是由![]() 的变化而引起的,
的变化而引起的,![]() 叫做函数
叫做函数![]() 的振幅.
的振幅.![]() ,
,![]() 的值域是
的值域是![]() ,最大值是
,最大值是![]() ,最小值是
,最小值是![]() .
.
(2)函数![]() 与
与![]() 的图像的联系
的图像的联系
【例2】作函数![]() 及
及![]() 的简图.
的简图.
解:函数![]() 的周期
的周期![]() ,因此,我们先来作
,因此,我们先来作![]() 时函数的简图.
时函数的简图.
列表:
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
1 |
0 |
-1 |
0 |
函数![]() 的周期
的周期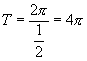 ,因此,我们先作
,因此,我们先作![]() 时函数的简图.
时函数的简图.
列表:
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
1 |
0 |
-1 |
0 |
描点作图(图2)
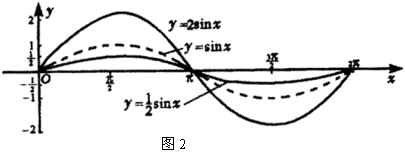
师:利用函数的周期性,我们可将上面的简图向左、右扩展,得出![]() ,
,![]() 及
及![]() ,
,![]() 的简图.
的简图.
请同学们观察函数![]() 与
与![]() 的图像间的联系及
的图像间的联系及![]() 与
与![]() 的图像间的联系.
的图像间的联系.
生:在函数![]() ,
,![]() 的图像上,横坐标为
的图像上,横坐标为![]() (
(![]() )的点的纵坐标同
)的点的纵坐标同![]() 上横坐标为
上横坐标为![]() 的点的纵坐标相等,因此
的点的纵坐标相等,因此![]() 的图像可以看做是把
的图像可以看做是把![]() 的图像上所有点的横坐标缩短到原来的
的图像上所有点的横坐标缩短到原来的![]() 倍(纵坐标不变)而得到的.
倍(纵坐标不变)而得到的.
同样,![]() 的图像可以看做把
的图像可以看做把![]() 的图像上所有点的横坐标伸长为原来的2倍(纵坐标不变)而得到的.
的图像上所有点的横坐标伸长为原来的2倍(纵坐标不变)而得到的.
师:由例2中,![]() 、
、![]() 与
与![]() 的图像的联系,请你探求函数
的图像的联系,请你探求函数![]() (
(![]() 且
且![]() )的图像与
)的图像与![]() 之间在联系.
之间在联系.
生:函数![]() (
(![]() 且
且![]() )的图像,可以看做是把
)的图像,可以看做是把![]() 的图像上所有点的横坐标缩短(当
的图像上所有点的横坐标缩短(当![]() 时)或伸长(当
时)或伸长(当![]() 时)到原来的
时)到原来的![]() 倍(纵坐标不变)而得到的.这种变换称为周期变换,它是由
倍(纵坐标不变)而得到的.这种变换称为周期变换,它是由![]() 的变化而引起的,
的变化而引起的,![]() 与周期
与周期![]() 的关系为
的关系为![]() .
.
3.演练反馈(投影)
1.画出下列函数在长为一周期的闭区间上的简图
(1)![]()
![]() (2)
(2)![]()
2.函数![]() ,
,![]() 的周期是什么?它的图像与正弦曲线有什么联系.
的周期是什么?它的图像与正弦曲线有什么联系.
3.说明如何由![]() ;由
;由![]()
参考答案:
1.
2.周期是![]() ,把
,把![]() 的图像上每个点的横坐标伸长
的图像上每个点的横坐标伸长![]() 倍(纵坐标不变)即得
倍(纵坐标不变)即得![]() 的图像.
的图像.
3.![]() 的图像沿
的图像沿![]() 轴方向压缩
轴方向压缩![]() 得
得![]() 的图像(纵坐标不变);把
的图像(纵坐标不变);把![]() 的图像上纵坐标缩短
的图像上纵坐标缩短![]() 倍(横坐标不变),即得
倍(横坐标不变),即得![]() 的图像.
的图像.
4.总结提炼
(1)用“五点法”作![]() 或
或![]() 的简图时,先要确定周期,再将周期四等份,找出五个关键点:0,
的简图时,先要确定周期,再将周期四等份,找出五个关键点:0,![]() ,
,![]() ,
,![]() ,
,![]() ,然后再列表、描点、作光滑曲线连接五个点.
,然后再列表、描点、作光滑曲线连接五个点.
(2)![]() 的图像可以看做是把正弦曲线
的图像可以看做是把正弦曲线![]() 图像经过振幅变换而得到.
图像经过振幅变换而得到.
(3)函数![]() 的图像可以看作是把
的图像可以看作是把![]() 实施周期变换而得.
实施周期变换而得.
(4)作图时,要注意坐标轴刻度,![]() 轴是实数轴,角一律用弧度制.
轴是实数轴,角一律用弧度制.
(四)板书设计
|
1.函数 例1 联系 2.函数
|
例2 联系 小结:演练反馈 总结提炼 |
(一)教学具准备
直尺、投影仪.
(二)教学目标
1.掌握由![]() 的变化过程,理解由
的变化过程,理解由![]() 到
到![]() 的变换步骤.
的变换步骤.
2.利用平移、伸缩变换方法,作函数![]() 图像.
图像.
(三)教学过程
1.设置情境
师:上节课,我们学习了如何由![]() 的图像通过变换得到
的图像通过变换得到![]() 和
和![]() 的图像,请同学复述一下变换的具体过程.
的图像,请同学复述一下变换的具体过程.
生:将![]() 的图像通过振幅变换便得到
的图像通过振幅变换便得到![]() 的图像
的图像
将![]() 的图像通过周期变换就得到
的图像通过周期变换就得到![]() 的图像
的图像
师:今天这节课,我们将继续学习如何由![]() 的图像通过变换手段分别得到
的图像通过变换手段分别得到![]() 及
及![]() 的图像,(板书课题:函数
的图像,(板书课题:函数![]() 和
和![]() 的图像)
的图像)
2.探索研究
(1)如何由![]() 的图像通过变换得到
的图像通过变换得到![]() 的图像
的图像
【例1】画出函数![]() ,
,![]() ,
,![]() ,
,![]() 的简图
的简图
师:由上一节画余弦函数的图像可知,函数![]() ,
,![]() 的图像可以看做把正弦曲线上所有的点向左平行移动
的图像可以看做把正弦曲线上所有的点向左平行移动![]() 个单位长度而得到.
个单位长度而得到.
同学们能否用类比的方法由![]() 的图像得到
的图像得到![]() 和
和![]() 的图像.
的图像.
生:从![]() 的图像向左平移
的图像向左平移![]() 个单位长度而得到
个单位长度而得到![]() ,即
,即![]() 的图像得到启发,我们只要把正弦曲线上所有的点向左平行移动
的图像得到启发,我们只要把正弦曲线上所有的点向左平行移动![]() 个单位长度,就可以得到
个单位长度,就可以得到![]() 的图像,如把正弦曲线上所有的点向右平移
的图像,如把正弦曲线上所有的点向右平移![]() 个单位长度,就可以得到
个单位长度,就可以得到![]() 的图像.
的图像.
函数 ![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
在一个周期内的图像如图1所示:(用叠放投影胶片,依次叠放三个函数图像)
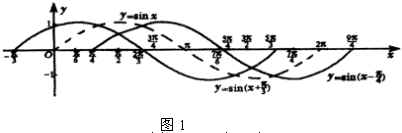
师:我们已经学过并且知道![]() 与
与![]() 图像是一种左、右平移关系,从例1中你能得到
图像是一种左、右平移关系,从例1中你能得到![]() 与
与![]() 的图像之间的联系吗?
的图像之间的联系吗?
生:函数![]() ,
,![]() (其中
(其中![]() )的图像可以看做把
)的图像可以看做把![]() 的图像上所有的点向左(当
的图像上所有的点向左(当![]() 时)或向右(当
时)或向右(当![]() 时)平行移动
时)平行移动![]() 个单位长度而得到的,这种变换叫做平移变换.
个单位长度而得到的,这种变换叫做平移变换.
(2)如何由![]() 的图像通过变换得到
的图像通过变换得到![]() 的图像
的图像
【例2】画出函数![]() ,
,![]() 的简图.
的简图.
解:函数![]() 的周期
的周期![]() ,我们先画出它的长度为一个周期的闭区间上的简图.
,我们先画出它的长度为一个周期的闭区间上的简图.
列表
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
3 |
0 |
-3 |
0 |
描点,连线得图2
利用函数的周期性,我们可以把它在![]() 上的简图向左、右分别扩展,从而得到它的简图.(用依次叠放投影片的方法投影展示上图)
上的简图向左、右分别扩展,从而得到它的简图.(用依次叠放投影片的方法投影展示上图)
师:函数![]() ,
,![]() 的图像,可以看作用下面的方法得到:先将
的图像,可以看作用下面的方法得到:先将![]() 上所有的点向左平移
上所有的点向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() ,
,![]() 的图像;再把后者所有点的横坐标缩短到原来的
的图像;再把后者所有点的横坐标缩短到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() ,
,![]() 的图像;再把所得到图像上所有点的纵坐标伸长到原来的3倍(横坐标不变),从而得到函数
的图像;再把所得到图像上所有点的纵坐标伸长到原来的3倍(横坐标不变),从而得到函数![]() ,
,![]() 的图像.
的图像.
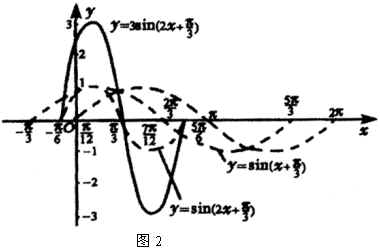
师:我们已经知道函数![]() 与
与![]() 是一种延
是一种延![]() 轴方向上的伸缩变换,从例2中你能得到
轴方向上的伸缩变换,从例2中你能得到![]() 与
与![]() 的图像之间的联系吗?
的图像之间的联系吗?
生:函数![]() ,
,![]() (其中
(其中![]() ,
,![]() )的图像,可以看作用下面的方法得到:先把正弦曲线上所有的点向左(当
)的图像,可以看作用下面的方法得到:先把正弦曲线上所有的点向左(当![]() 时)或向右(当
时)或向右(当![]() 时)平行移动
时)平行移动![]() 个单位长度,再把所得各点的横坐标缩短(当
个单位长度,再把所得各点的横坐标缩短(当![]() 时)或伸长(当
时)或伸长(当![]() 时)到原来的
时)到原来的![]() 倍(纵坐标不变),再把所得各点的纵坐标伸长(当
倍(纵坐标不变),再把所得各点的纵坐标伸长(当![]() 时)或缩短(当
时)或缩短(当![]() 时)到原来的
时)到原来的![]() 倍(横坐标不变).
倍(横坐标不变).
我们小结一下上述步骤如下:
师:其步骤流程图如下:
![]()
这一过程体现了由简单到复杂,特殊到一般的化归思想.
函数![]() ,
,![]() (其中
(其中![]() ,
,![]() )的简图,可以用类似方法画出.
)的简图,可以用类似方法画出.
(3)![]() 、
、![]() 、
、![]() 的物理意义
的物理意义
当函数![]() ,
,![]() (其中
(其中![]() ,
,![]() )表示一个振动量时,
)表示一个振动量时,![]() 就表示这个量振动时离开平衡位置的最大距离,通常称为这个振动的振幅.
就表示这个量振动时离开平衡位置的最大距离,通常称为这个振动的振幅.
往复振动一次所需要的时间![]() ,称为这个振动的周期;单位时间内往复振动的次数
,称为这个振动的周期;单位时间内往复振动的次数![]() 称为振动的频率.
称为振动的频率.
![]() 称为相位;
称为相位;![]() 时的相位
时的相位![]() 称为初相.
称为初相.
3.演练反馈(投影)
(1)要得到函数![]() 图像,只需将
图像,只需将![]() 的图像(
)
的图像(
)
A.向右平移![]() B.向左平移
B.向左平移![]() C.向右平移
C.向右平移![]() D.向左平移
D.向左平移![]()
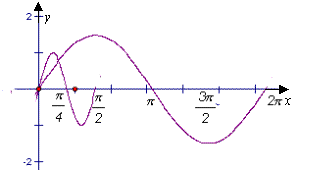
(2)函数![]() 的一个周期内图像如图3.
的一个周期内图像如图3.
则![]() 的表达式
的表达式 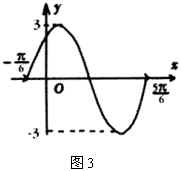
A.![]()
B.![]()
C.![]()
D.![]()
(3)把函数![]() 的图像向左平移
的图像向左平移![]() 个单位,再把图像上各点的横坐标压缩为原来的
个单位,再把图像上各点的横坐标压缩为原来的![]() ,所得的解析式为_________.
,所得的解析式为_________.
参考答案:
(1)C.把![]() 右移
右移![]() ,得
,得![]()
(2)D.因为![]() ,又
,又![]() 与
与![]() 比较知,是其左移
比较知,是其左移![]() 而得,即
而得,即![]()
(3)变换过程如下:第一步得:![]()
第二步得:![]()
4.总结提炼
(1)了解三角函数图像的变化规律和方法,由![]() ,此步骤只是平移(
,此步骤只是平移(![]() ,左移
,左移![]() 个单位;
个单位;![]() ,右移
,右移![]() 个单位),而由
个单位),而由![]() 可由二条思路:
可由二条思路:
①![]() 即先平移后压缩.
即先平移后压缩.
②![]() 即先压缩再平移.
即先压缩再平移.
不论哪一条路径,每一次变换都是对一个字母![]() 而言的,如,
而言的,如,![]() 的图像向右平移
的图像向右平移![]() 个单位,得到的应是
个单位,得到的应是![]() ,而不是
,而不是![]() ;又
;又![]() 的图像横坐标扩大到原来的2倍,应是
的图像横坐标扩大到原来的2倍,应是![]() 而不是
而不是![]() .
.
(2)作函数图像的方法有多种,如描点法,五点作图法,根据奇、偶利用对称法等等,平移、变换法只是诸多作图法中一种,它与五点作图法同样重要,希望大家多练习,掌握变换次序上的技巧.
(四)板书设计
|
课题________ 1.如何由 作 例1 2.如何由 作 例2 |
变换法作 演练反馈 总结提炼 |