第七节 二倍角的正弦、余弦、正切

教学设计示例（一）

二倍角的正弦、余弦、正切（第一课时）

（一）教学具准备
　　投影仪或多媒体设备

（二）教学目标
　　1．掌握 、 、 公式的推导，明确 的取值范围．
　　2．运用二倍角公式求三角函数值．

（三）教学过程
1．设置情境
　　师：我们已经学习了两角和与差的正弦、余弦、正切公式，请大家回忆一下这组公式的来龙去脉，并请一个同学把这六个公式写在黑板上，
　　生：
　　　　
　　　　
　　　　
　　师：很好，对于这些公式大家一方面要从公式的推导上去理解它，另一方面要从公式的结构特点上去记忆，还要注意公式的正用、逆用和变用．今天，我们继续学习二倍角的正弦、余弦和正切公式
2．探索研究
　　师：请大家想一想，在公式 、 、 中对 、 如何合理赋值，才能出现 、 、 的表达式，并请同学把对应的等式写在黑板上．
　　生：可在 、 、 中，令 ，就能出现 、 、 ，对应表达式为：
　　　　
　　　　
　　　　
　　即：
　　　　
　　　　
　　师：很好，看来本节课的主要任务，已经被大家轻松完成了．对于公式 ，我们似乎要注意些什么？大家想一想要关注什么？
　　生：要使 有意义及 ， 有意义．
　　师： 有意义即 ， ．
　　 ，即 ，也就是 ，可变为 ．
　　要使 有意义，则须 ．
　　综合起来就是 ，且 ， ．当 时，虽然 的值不存在，但 的值是存在的，这时求 的值可利用诱导公式，即 ．
　　师：对于 ，还有没有其他的形式？
　　生：有（板书）
　　∵    ∴ 或
　　∴
　　师：（板书三个公式，并告诉学生公式记号分别为 、 、 ）对二倍角公式大家要注意以下问题．（1）用 和 表示 、 ，用 表示 ，即用单角的三角函数表示复角的三角函数．（2） 有三种形式， 是有条件的．
3．例题分析
　　【例1】已知 ， ．求 ， ， 的值．
　　解：因为 ， ．所以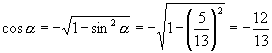
　　　　于是
　　　　　　
　　　　　　
　　说明：本题也可按下列程序来做，请大家比较方法之优劣．
　　∵ ，
　　∴ ，且 ，
　　
　　　　　　
　　　　　　

　　　　
　　　　

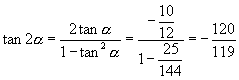
【例2】不查表求值：
　　（1） ；　　（2） ；
　　（3） ；　　　　　（4） ．
解：（1）
　　　　　　　　　　　  

　　（2）
　　　　　　　　　　　
　　　　　　　　　　　
　　　　　　　　　　　

　　（3）
　　（4）
　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　
　　说明：逆用公式的先决条件是认识公式的本质，要善于把表象的东西拿开，正确捕捉公式原形以便合理运用公式．

【例3】 求证：
　　引导学生观察式子两边的结构，提出证题的方向．
　　生：左边都是单角的三角函数，右边是二倍角．又因左边比右边明显复杂得多，所以应由左边证向右边，注意把单角的三角函数变为二倍角．
　　师：（板书）
证明：左边
　　　　　
　　　　　
　　　　　 右边
所以原式成立

【例4】化简： ．
　　师：这道题给我们的感觉是有些无从下手，很难看出有什么公式可以直接使用．两个角 与 似乎还有一线希望，但由于受函数名称限制难以发挥它的作用，大家都来想想看，有什么办法可以打破这一僵局（请同学们讨论）？
　　生：在同角三角函数的化简中，如果一个式子有弦、有切，我们可以把切化成弦．
　　师：好的，我们来尝试（板书）
　　解：
　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　
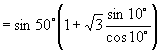
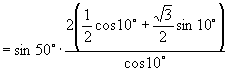
　　说明：本题在尝试把正切化为弦（正、余弦）后果然获得成功，其实把正切化为弦就是一条重要思想，请同学们切记“遇切、割化弦”这一规律．另外本题的解答过程还反映了逆用和角公式的重要性．希望大家一并记下．

练习（投影）

（1）化简
（2）
（3）若 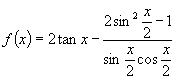，则
答案：（1） ；（2） ；（3）8

4．总结提炼

　　（1）在两角和的三角函数公式 、 、 中，当 时，就可以得到二倍角的三角函数公式 、 、 ，说明后者是前者的特例．
　　（2） 、 中角 没有限制条件，而 中，只有 和 时，才成立．
　　（3）二倍角公式不仅限于 是 的二倍形式，其他如 是 的2倍， 是 的二倍， 是 的二倍等等都是适用的，要熟悉这些多种形式的两个角的倍数关系，才能熟练地应用好二倍角公式，这是灵活运用公式的关键．
　　 有三种形式 ，要依据条件，灵活选用公式．另外，逆用此公式时，更要注意结构形式．

（四）板书设计

教学设计示例（二）

4.7二倍角的正弦、余弦、正切（第二课时）

（一）教学具准备
　　投影仪

（二）教学目标
　　1．应用倍角公式解决本章开头的一个应用问题．
　　2．活用倍角公式，推求半角公式．

（三）教学过程
1．设置情境
　　请同学看教材第3页上的一段文字，它叙述的是一个生活中的实际问题：
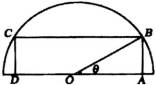“如图1，是一块以点 为圆心的半圆形空地，要在这块空地上画出一个内接矩形 辟为绿地，使其一边 落在半圆的直径上，另两点 、 落在半圆的圆周上．已知半圆的半径为 ，如何选择关于点 对称的点 、 的位置，可以使矩形 的面积最大？”根据教材提示应用所学的倍角公式，同学们能尝试解答它吗？
2．探索研究
　　分析：要使矩形 的面积最大，就必须想办法把面积表示出来，不妨利用我们所学的三角知识，从角的方面进行考虑，设 ，则 ， ，所以 可以用 表示．
解：设   则  
　　
　　∵   ∴
　　当 时，    即 ，
　　这时  ，
答：点 、 分别位于点 的左、右方 处时 取得最大值 ．
　　变式：把一段半径为 的圆木锯成横截面为矩形的木料，怎样锯法才能使横截面的面积最大？
　　生：根据上题的结果可知这时圆内接矩形为内接正方形时面积最大．
　　以上是倍角公式在实际生活中的运用，请同学们观察以下例题，并分析、思考后能否得出证明．
3．例题分析
【例1】求证：
　　（1） ；（2） ；
　　（3） ．
思考，讨论．
　　我们知道公式 中 是任意的，所以我们可以用 来替换 ，这样就得到
　　
　　
　　即            
　　　　
　　上面三式左边都是平方形式，当 的值已知， 角的终边所在象限已知时，就可以将右边开方，从而求得：
　　          
以上两式相除又得：
　　　　　　
　　这三个式子称之为半角公式，“±”号的取舍得由 终边所在象限确定．

【例2】求证：
　　 ．
　　分析：从例1引出例2， ，右边是同一个三角函数，并且还要附上正负号，而所要证明的式子右边有两个三角函数，不带正负号．故我们不能利用上法，得另想办法．
　　师：（边叙述边板书）
　　
　　
　　∴
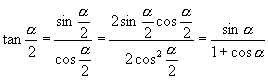
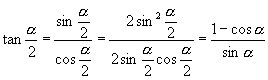
　　上式不含根号也不必考虑“±”号选取，通常用于化简或证明三角恒等式，同样可作半角公式运用．

【例3】已知： ，求 ， ， ．
　　解：
　　　　
　　　　
　　说明：①例1中（1）、（2）两式使用频率极高，正、逆使用都非常普遍．习惯从左到右，常称“扩角降幂公式”，从右到左常谓“缩角升幂公式”，
　　②半角公式是二倍角公式的另一种表达方式，倍半关系是相对的．
练习（投影）
　　1．已知：       （ ），
　　　求：（1） ；（2） ．
　　2．若 ，求： 的值．
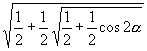　　3．求： 的值．

参考答案：
解：1．∵
　　两边平方得              ∴
　　又∵         ∴
　　　∴          ∴
　　2．∵     ∴
　　　原式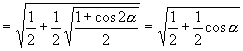
　　（3）
　　　　
　　　　
　　　　
　　　　
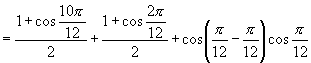
另解：设  ……………………①
　　　　　 ……………………②
　　①＋②得 …………………………③
　　①－②得 ……④
　　③＋④得     ∴
4．总结提炼
　　（1）本节课我们由倍角公式出发解决了实际应用问题，得出结论“在一个圆的所有内接矩形中，以内接正方形的面积为最大”，另外由倍角公式解答了例1、例2，从而推导出半角公式，公式“±”号的选取决定于 终边所在的象限，例2的应用也很广泛，大家可根据题目的条件选择使用较为方便的形式．
　　（2）从半角公式可以看出，半角的正弦、余弦、正切公式都可以用单角的余弦来表示．
　　（3）若给出的 是象限角，则可根据下表决定符号．

　　若给出的 是区间角，则先求 所在区间再确定符号．
　　若没有给出确定符号的条件，则应在根号前保留“±”号．

（五）板书设计