 设为首页
设为首页
 加入收藏
加入收藏
教学设计示例
4.6两角和与差的正弦、余弦、正切(第一课时)
(一)教具准备
直尺、圆规、投影仪
(二)教学目标
1.掌握 ![]() 公式的推导,并能用赋值法,求出公式
公式的推导,并能用赋值法,求出公式 ![]() .
.
2.应用公式 ![]() ,求三角函数值.
,求三角函数值.
(三)教学过程
1.设置情境
上一单元我们学习了同一个角的三角函数的性质以及各三角函数之间的相互关系.本节开始讨论两个角的三角函数,已知任意角 ![]() 的三角函数值,如何求出
的三角函数值,如何求出 ![]() ,
, ![]() 或
或 ![]() 的三角函数值,这一节课我们将研究
的三角函数值,这一节课我们将研究 ![]() 、
、 ![]() .
.
2.探索研究
(1)公式 ![]() 、
、 ![]() 推导.
推导.
请大家考虑,如果已知 ![]() 、
、 ![]() ,怎样求出
,怎样求出 ![]() ?
?
![]() 是否成立.
是否成立.
生:不成立, ![]() ,
, ![]() 等式就不成立.
等式就不成立.
师:很好,把 ![]() 写成
写成 ![]() 是想应用乘法对加法的分配律,可是
是想应用乘法对加法的分配律,可是 ![]() 是角
是角 ![]() 的余弦值,并不是“
的余弦值,并不是“ ![]() ”乘以
”乘以 ![]() ,不能应用分配律.
,不能应用分配律.
事实上如果 ![]() 都是锐角,那么总有
都是锐角,那么总有 ![]() .
.
考虑两组数据
① ![]() ,
,
![]() 这时
这时 ![]() ,
, ![]() 而
而 ![]()
② ![]() ,
,
![]() 这时
这时 ![]() ,
, ![]() 而
而 ![]()
从这组数据我们发现不能由 ![]() 、
、 ![]() 直接得出
直接得出 ![]() .师:如果我们再算出
.师:如果我们再算出 ![]() ,
, ![]() ,试试看能否找到什么关系.
,试试看能否找到什么关系.
生:① ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() 而
而 ![]()
② ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() 而
而 ![]()
由(1)、(2)可得出, ![]()
师:这位同学用具体的例子得到的一个关系式:
![]()

只有通过严格的理论证明才行.下面给出证明:为了证明它,首先给出两点间的距离,图1(也可以利用多媒体课件演示).考虑坐标平面内的任意两点
![]() ,
, ![]() 过点
过点 ![]() 分别作
分别作 ![]() 轴的垂线
轴的垂线 ![]() ,
, ![]() ,与
,与 ![]() 轴交于点
轴交于点 ![]() ,
, ![]() ;同理
;同理 ![]() ,
,
![]() 那么
那么 ![]() ,
, ![]() ,由勾股定理
,由勾股定理 ![]() ,由此得到平面内
,由此得到平面内 ![]()
![]() 两点间的距离公式
两点间的距离公式
|
|
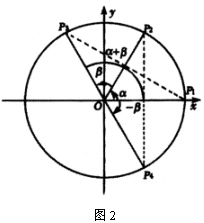
师:(可以用课件演示)如右图2,在直角坐标系 ![]() 内作单位圆
内作单位圆 ![]() ,并作出角
,并作出角 ![]() 、
、 ![]() 与
与 ![]() 请同学们把坐标系中
请同学们把坐标系中 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 各点的坐标用三角函数表示出来.
各点的坐标用三角函数表示出来.
生: ![]() ,
, ![]() ,
, ![]() ,
, ![]()
师:线段 ![]() 与
与 ![]() 有什么关系?为什么?
有什么关系?为什么?
生:因为△ ![]() ≌△
≌△ ![]() ,所以
,所以 ![]() .
.
师:请同学们用两点间的距离公式把 ![]() 表示出来并加以整理.
表示出来并加以整理.
![]()
展开并整理,得
![]()
所以
![]() (记为
(记为 ![]() )
)
这个公式对任意的 ![]() ,
, ![]() 均成立,如果我们把公式中的
均成立,如果我们把公式中的 ![]() 都换成
都换成 ![]() ,又会得到什么?
,又会得到什么?
生: ![]()
即
![]()
(记为 ![]() )
)
(2)例题分析
【例1】不查表,求 ![]() 及
及 ![]() 的值.
的值.
因为题目要求不查表,所以要想办法用特殊角计算,为此 ![]() 化成
化成 ![]() ,
, ![]() 化成
化成 ![]() ,请同学们自己利用公式计算.
,请同学们自己利用公式计算.
注:拆角方法并不惟一.事实上,如果求出 ![]() ,那么
,那么 ![]() ,再者,
,再者, ![]() 也可写成
也可写成 ![]() ,甚至
,甚至 ![]() 等均可以.
等均可以.
【例2】已知 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求
,求 ![]() 的值.
的值.
分析:观察公式 ![]() 要算
要算 ![]() 应先求出
应先求出 ![]() ,
, ![]() .
.
解:由 ![]() ,
, ![]() 得
得
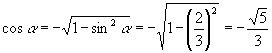
又由 ![]() ,
, ![]() 得
得
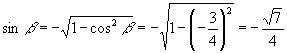
![]()
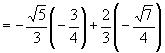
![]()
【例3】 不查表,求下列各式的值:
(1) ![]() ;
;
(2) ![]() ;
;
(3) ![]() .
.
解:(1) ![]()
![]()
(2) ![]()
![]()
![]()
(3) ![]()
![]()
![]()
【例4】 证明公式:
(1) ![]() ;(2)
;(2) ![]()
证明:(1)利用 ![]() 可得
可得
![]()
![]()
∴ ![]()
(2)因为上式中 ![]() 为任意角,故可将
为任意角,故可将 ![]() 换成
换成 ![]() ,就得
,就得
![]()
即
![]()
练习(投影、学生板演)
(1) ![]()
(2)已知 ![]() ,
, ![]() ,求
,求 ![]()
解答:
(1)逆用公式 ![]()
![]()
![]()
(2)凑角:∵ ![]() ,∴
,∴ ![]() ,故
,故
![]()
![]() .
.
说明:请同学们很好体会一下,上述凑角的必然性和技巧性,并能主动尝试训练,以求熟练。
3.演练反馈
(1) ![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
(2) ![]() 等于( )
等于( )
A.0 B. ![]() C.
C. ![]() D.2
D.2
(3)已知锐角 ![]() 满足
满足 ![]() ,
, ![]() ,则
,则 ![]() 为(
)
为(
)
A. ![]() B.
B. ![]() C.
C. ![]() 或
或
![]() D.
D. ![]() ,
, ![]()
参考答案:(1)B; (2)B; (3)A.
4.总结提炼
(1)牢记公式“ ![]() ”结构,不符合条件的要能通过诱导公式进行变形,使之符合公式结构,即创造条件用公式.
”结构,不符合条件的要能通过诱导公式进行变形,使之符合公式结构,即创造条件用公式.
(2)在“给值求值”题型中,要能灵活处理已、未知关系,如已知角 ![]() 、
、![]() 的值,求
的值,求 ![]() ,应视
,应视 ![]() 、
、 ![]() 分别为已知角,
分别为已知角, ![]() 为未知角,并实现“
为未知角,并实现“ ![]() ”与“
”与“ ![]() ”及“
”及“ ![]() ”之间的沟通:
”之间的沟通: ![]() .
.
(3)利用特值代换证明 ![]() ,
, ![]() ,体会
,体会![]() 的强大功能.
的强大功能.
(四)板书设计
|
1.平面内两点间距离公式 2.两角和余弦公式及推导 |
例1 例2 例3 |
例4 练习反馈 总结提炼 |
教学设计示例
4.6两角和与差的正弦、余弦、正切(第二课时)
(一)教学具准备
投影仪
(二)教学目标
1.掌握利用 ![]() 得到的两角和与差的正弦公式.
得到的两角和与差的正弦公式.
2.运用 ![]() 公式进行三角式的求值、化简及证明.
公式进行三角式的求值、化简及证明.
(三)教学过程
1.已知 ![]() 两角,我们可以利用
两角,我们可以利用 ![]() 的三角函数去计算复合角
的三角函数去计算复合角 ![]() 的余弦,那么,我们能否用
的余弦,那么,我们能否用 ![]() 的三角函数去表达复合角
的三角函数去表达复合角 ![]() 的正弦呢?本节课将研究这一问题.
的正弦呢?本节课将研究这一问题.
2.探索研究
(1)请一位同学在黑板上写出 ![]() ,
, ![]() 的展开式.
的展开式.
![]()
![]() .
.
由于公式中的 ![]() 是任意实数,故我们对
是任意实数,故我们对 ![]() 实施特值代换后并不影响等号成立,为此我们曾令
实施特值代换后并不影响等号成立,为此我们曾令 ![]() ,得到
,得到 ![]() ,
,
![]() 两个熟悉的诱导公式,请同学们尝试一下,能否在
两个熟悉的诱导公式,请同学们尝试一下,能否在 ![]() 中对
中对 ![]() 选取特殊实数代换,使
选取特殊实数代换,使 ![]() 诱变成
诱变成 ![]() 呢?或者说能否把
呢?或者说能否把 ![]() 改成用余弦函数来表示呢?请同学回答.
改成用余弦函数来表示呢?请同学回答.
生:可以,因为 ![]()
该同学的思路非常科学,这样就把新问题 ![]() 问题化归为老问题:
问题化归为老问题: ![]() .
.
事实上:
![]() (视“
(视“ ![]() ”为
”为 ![]() )
)
![]()
![]()
这样,我们便得到公式.
![]() 简化为
简化为 ![]() .
.
由于公式中的 ![]() 仍然是一切实数,请同学们再想一下,如何获得
仍然是一切实数,请同学们再想一下,如何获得 ![]() 的展开式呢?请同学回答.
的展开式呢?请同学回答.
生:只要在公式 ![]() 中用
中用 ![]() 代替
代替 ![]() ,就可得到:
,就可得到:
![]()
即
![]()
师:由此得到两个公式:
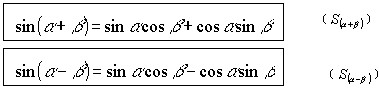
对于公式 ![]() 还可以这样来推导:
还可以这样来推导:
![]()
![]()
![]()
说明:
(1)上述四个公式 ![]() ,虽然形式、结构不同,但它们本质是相同的,因为它们同出一脉:
,虽然形式、结构不同,但它们本质是相同的,因为它们同出一脉:
![]()
![]()
![]()
![]()
这样我们只要牢固掌握“中心”公式 ![]() 的由来及表达方式,就掌握了其他三个公式了.这要作为一种数学思想、一个数学方法来仔细加以体会.
的由来及表达方式,就掌握了其他三个公式了.这要作为一种数学思想、一个数学方法来仔细加以体会.
(2) ![]() 、
、 ![]() 是用
是用 ![]() 的单角函数表达复合角
的单角函数表达复合角 ![]() 的正、余弦.反之,我们不得不注意,作为公式的逆用,我们也可以用复合角
的正、余弦.反之,我们不得不注意,作为公式的逆用,我们也可以用复合角 ![]() 的三角函数来表达单角三角函数.诸如:
的三角函数来表达单角三角函数.诸如: ![]() ,
, ![]() ,
, ![]() 及
及 ![]() 四种表达式,实质上是方程思想的体现:
四种表达式,实质上是方程思想的体现:
由 ![]() 得:
得:
![]() ①
①
由 ![]() 得
得
![]() ②
②
由 ![]() ,得:
,得:
![]() ③
③
由 ![]() 得:
得:
![]() ④
④
等式①、②、③、④在求值、证明恒等式中无疑作用是十分重大的.
(2)例题分析
【例1】 不查表,求 ![]() ,
, ![]() 的值.
的值.
解: ![]()
![]()
![]()
说明:我们也可以用 ![]() 系统来做:
系统来做:
![]()
![]()
![]()
![]()
![]()
【例2】已知, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 求,
求, ![]() .
.
分析:观察公式 ![]() 和本题的条件,必须先算出
和本题的条件,必须先算出 ![]() ,
, ![]()
解:由 ![]() ,
, ![]() 得
得
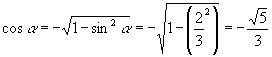
又由 ![]() ,
, ![]() 得
得
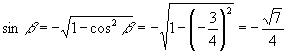
∴ ![]()
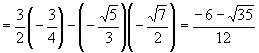
【例3】不查表求值:
(1) ![]() ;
;
(2) ![]() .
.
解:(1) ![]()
![]()
![]()
![]()
(2) ![]()
![]()
![]()
![]()
![]()
练习(投影)
(1) ![]() ,
, ![]() ,则
,则 ![]() .
.
(2)在△ ![]() 中,若
中,若 ![]() ,则△
,则△ ![]() 是___________.
是___________.
参考答案:
(1)∴ ![]()
![]()
∴ ![]()
(2)由 ![]() ,
, ![]()
∴ ![]()
∴ ![]() ,
, ![]() 为钝角,即△
为钝角,即△ ![]() 是钝角三角形.
是钝角三角形.
【例4】求证: ![]() .
.
分析:我们从角入手来分析,易见左边有复角(即两角和与差)右边全是单角,所以思路明确,就是要把复角变单角.
证明:
左边 ![]()
![]()
![]()
![]() 右
∴原式成立
右
∴原式成立
如果我们本着逆用公式来看待本题,那么还可这样想:
由 ![]()
![]()
令 ![]() ,
, ![]() 则
则
![]() ①
①
至于
![]()
![]()
我们可这样分析:
∵ ![]()
令 ![]() 得
得
![]()
![]()
同理 ![]()
∴①可进一步改写为:
![]()
![]()
∴ ![]() ……②
……②
又∵
![]()
![]()
![]()
![]()
![]() ……③
……③
由②、③得
![]()
本题还可以从函数名称来分析,左边是正、余弦函数,右边是正切函数,故可考虑从右边入手用化弦法,请同学们自己把上面过程反过来,从右边推出左边.
【例5】求证: ![]()
师:本题我们可以从角的形式来分析,左边是单角,右边是复角,如果从右边证左边则要把复角变单角(即利用和角公式);如果从左边证右边则须配一个角 ![]() ,所以本题起码有两种证法.
,所以本题起码有两种证法.
证法1:右边 ![]()
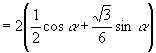
![]() 左边
左边
∴原式成立
师:另一种证法根据刚才的分析要配出角 ![]() ,怎样配?大家仔细观察证法一就不难发现了.
,怎样配?大家仔细观察证法一就不难发现了.
证法2:(学生板书)
左边 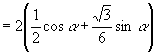
![]()
![]() 右边
∴原式成立
右边
∴原式成立
3.演练反馈(投影)
(1)化简 ![]()
(2)已知 ![]() ,则
,则 ![]() 的值(
)
的值(
)
A.不确定,可在[0、1]内取值 B.不确定,可在[-1、1]中取值
C.确定,等于1 D.确定,等于1或-1
参考答案:
(1)原式
![]()
![]()
![]()
![]()
(2)C
4.总结提炼
(1)利用“拆角”“凑角”变换是进行三角函数式求值、证明、化简的常用技巧,如: ![]() ,
, ![]() ,
, ![]() .在三角形中,
.在三角形中, ![]() ,
, ![]() 等变换技巧,同学们应十分熟悉.
等变换技巧,同学们应十分熟悉.
(2)本节课的例5,代表着一类重要题型,同学们要学习它的凑角方法,一般地
![]() ,其中
,其中 ![]() .
.
(3)在恒等式中,实施特值代换,是一类重要的数学方法——母函数法,这种方法在数学的其他学科中,均有用武之地。它反映的是特殊与一般的辨证统一关系.
(四)板书设计
|
课题:两角和与差的正弦 1.公式推导 ① =…… 把公式中 2.公式的结构特点 中的运算符号一致(区别于 3.折、凑角技巧 |
例1 例2 例3 |
例4 例5 演练反馈 总结提炼 |