 设为首页
设为首页
 加入收藏
加入收藏
正弦、余弦的诱导公式教学设计示例(一)
教学目标:
1.掌握诱导公式及其推演时过程.
2.会应用诱导公式,进行简单的求值或化简.
教学重点:
理解并掌握诱导公式.
教学难点:
运用诱导公式求三角函数值,化简或证明三角函数式.
教学用具:
三角板、圆规、投影仪.
教学过程:
1.设置情境
我们已经学过了诱导公式一: ![]() ,
, ![]() ,
,![]() ,(
,( ![]() ),有了它就可以把任一角的三角函数求值问题,转化为
),有了它就可以把任一角的三角函数求值问题,转化为
![]() ~
~ ![]() 间角的三角函数值问题.那么能否再把
间角的三角函数值问题.那么能否再把 ![]() ~
~ ![]() 间的角的三角函数求值,继续化为我们熟悉的
间的角的三角函数求值,继续化为我们熟悉的 ![]() ~
~ ![]() 间的角的三角函数求值问题呢?如果能的话,那么任意角的三角函数求值,都可以化归为锐角三角函数求值,并通过查表方法而得到最终解决,本课就来讨论这一问题.
间的角的三角函数求值问题呢?如果能的话,那么任意角的三角函数求值,都可以化归为锐角三角函数求值,并通过查表方法而得到最终解决,本课就来讨论这一问题.
2.探索研究
(1)出示下列投影内容
设 ![]() ,对于任意一个
,对于任意一个 ![]() 到
到 ![]() 的角
的角 ![]() ,以下四种情形中有且仅有一种成立.
,以下四种情形中有且仅有一种成立.

首先讨论 ![]() ,其次讨论
,其次讨论 ![]() ,
, ![]() 以及
以及 ![]() 的三角函数值与
的三角函数值与 ![]() 的三角函数值之间的关系,为了使讨论更具一般性,这里假定
的三角函数值之间的关系,为了使讨论更具一般性,这里假定
![]() 为任意角.
为任意角.
(2)学习诱导公式二、三的推导过程.
已知任意角 ![]() 的终边与单位圆相交于点
的终边与单位圆相交于点 ![]() ,请同学们思考回答点
,请同学们思考回答点 ![]() 关于
关于 ![]() 轴、
轴、 ![]() 轴、原点对称的三个点的坐标间的关系.
轴、原点对称的三个点的坐标间的关系.
点 ![]() 关于
关于 ![]() 轴对称点
轴对称点 ![]() ,关于
,关于 ![]() 轴对称点
轴对称点 ![]() ,关于原点对称点
,关于原点对称点 ![]() (可利用演示课件).
(可利用演示课件).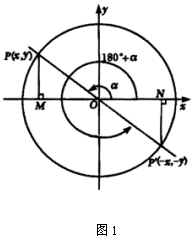
图1由于 ![]() 角的终边与单位圆交于
角的终边与单位圆交于 ![]() ,则
,则 ![]() 的终边就是角
的终边就是角 ![]() 终边的反向延长线,角
终边的反向延长线,角 ![]() 的终边与单位圆的交点为
的终边与单位圆的交点为 ![]() ,则
,则 ![]() 是与
是与 ![]() 关于
关于 ![]() 对称的点.所以
对称的点.所以 ![]() ,又因单位圆半径
,又因单位圆半径 ![]() ,由正弦函数、余弦函数定义,可得
,由正弦函数、余弦函数定义,可得
![]()
![]()
![]()
![]()
于是得到一组公式(公式二)
|
|
我们再来研究角 ![]() 与
与 ![]() 的三角函数值之间的关系,如图2,利用单位圆作出任意角
的三角函数值之间的关系,如图2,利用单位圆作出任意角
![]() 与单位圆相交于点
与单位圆相交于点 ![]() ,角
,角 ![]() 的终边与单位圆相交于点
的终边与单位圆相交于点 ![]() ,这两个角的终边关于
,这两个角的终边关于 ![]() 轴对称,所以
轴对称,所以 ![]()

∵ ![]()
∴ ![]()
![]()
于是又得到一组公式(公式三)
|
|
【例1】求下列三角函数值:
(1)![]() (2)
(2) ![]() ;
;
(3) ![]() ;(4)
;(4) ![]() .
.
解:(1)![]()
![]()
(2) ![]()
![]()
![]()
(3) ![]()
![]()
(4) ![]()
![]()
![]()
【例2】化简: ![]()
解:∵ ![]()
![]()
![]()
![]()
![]()
![]()
∴ 原式 ![]()
(3)推导诱导公式四、五
请同学们思考如何利用已学过的诱导公式推导 ![]() ,
, ![]() 与
与 ![]() 的三角函值之间的关系?由诱导公式我们可以得到
的三角函值之间的关系?由诱导公式我们可以得到
![]()
![]()
![]() :
: ![]()
![]()
由此可得公式四、五
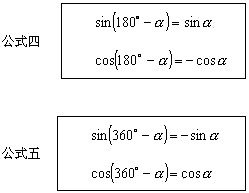
公式一、二、三、四、五都叫做诱导公式.概括如下: ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的三角函数值,等于
的三角函数值,等于 ![]() 的同名函数值,前面加上一个把
的同名函数值,前面加上一个把 ![]() 看成锐角时原函数值的符号,简化成“函数名不变,符号看象限”的口诀.
看成锐角时原函数值的符号,简化成“函数名不变,符号看象限”的口诀.
【例3】求下列各三角函数:
(1) ![]() ; (2)
; (2) ![]() .
.
解:(1) ![]()
![]()
![]()
(2) ![]()
![]()
![]() .
.
观察以上的解题过程,请同学们总结,利用诱导公式求任意角的三角函数值的步骤.
学生回答后老师总结得出,在求任意角的三角函数值时一般可按以下步骤:
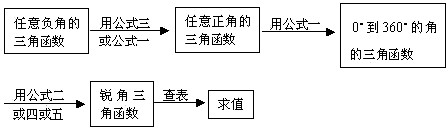
运用诱导公式解题的本质是多次运用“化归”思想方法,化负角为正角,化
![]() 到
到 ![]() 的角为
的角为 ![]() 到
到 ![]() 间的角,再求值的过程.
间的角,再求值的过程.
3.演练反馈(投影仪)
(1)已知 ![]() ,求
,求 ![]() 的值
的值
(2)已知 ![]() ,求
,求 ![]() 的值
的值
(3)已知 ![]() ,求
,求 ![]() 的值
的值
参考答案:
(1)若 ![]() 为Ⅳ象限角,则
为Ⅳ象限角,则 ![]()
若 ![]() 为Ⅰ象限角,则
为Ⅰ象限角,则 ![]()
(2) ![]()
(3)∵ ![]()
![]()
![]()
![]()
∴ ![]()
![]()
4.本课小结
(1)求任意角的三角函数式的一般程序:负(角)变正(角)→大(角)变小(角)→(一直)变到
![]() ~
~ ![]() 之间(能查表).
之间(能查表).
(2)变角是有一定技巧的,如 ![]() 可写成
可写成 ![]() ,也可以写成
,也可以写成 ![]() 不同表达方法,决定着使用不同的诱导公式.
不同表达方法,决定着使用不同的诱导公式.
(3)凑角方法也体现出很大技巧。如,已知角“ ![]() ”,求未知角“
”,求未知角“ ![]() ”,可把
”,可把 ![]() 改写成
改写成 ![]() .
.
课时作业:
1.已知 ![]() ,
, ![]() 是第四象限角,则
是第四象限角,则 ![]() 的值是(
)
的值是(
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.下列公式正确的是(
)
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
3. ![]() 的成立条件是(
)
的成立条件是(
)
A. ![]() 为不等于
为不等于 ![]() 的任意角 B.锐角
的任意角 B.锐角
C. ![]() D.
D. ![]() ,
, ![]() 且
且 ![]()
4.在 ![]() 中,下列各表达式为常数的是(
)
中,下列各表达式为常数的是(
)
A. ![]() B.
B. ![]()
C. ![]() D.
D.
![]()
5.化简
(1) ![]()
(2) ![]()
6.证明恒等式
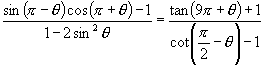
参考答案:
1.A; 2.D; 3.D; 4.C;
5.(1)0,(2) ![]() ;
;
6.左 ![]()
![]()
![]()
![]()
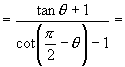 右
右
正弦、余弦的诱导公式教学设计示例(二)
教学目标:
1.在熟练掌握诱导公式一~五的基础上,再讨论![]() ,
,![]() 这三种形式的角的三角函数与
这三种形式的角的三角函数与![]() 角的三角函数之间关系。并把之当作“新”一组诱导公式.
角的三角函数之间关系。并把之当作“新”一组诱导公式.
2.利用诱导公式一~五及上述“新”诱导公式解决化简、求值、恒等式证明问题.
重点难点:
用诱导公式解决化简、求值、恒等式证明问题.
教学用具:
投影仪三
教学过程:
1.设置情境
我们已经知道![]() ,
,![]() ,那么
,那么![]() ,
,![]() 能否也能直接用
能否也能直接用![]() 的三角函数表达呢?本节课我们就
的三角函数表达呢?本节课我们就![]() ,
,![]() 这三种形式的角,讨论它们的三角函数值与
这三种形式的角,讨论它们的三角函数值与![]() 的三角函数值的关系,并把所得结果总结为一组“新”诱导公式。
的三角函数值的关系,并把所得结果总结为一组“新”诱导公式。
2.探索研究
(1)设![]()
![]() ,则对于任意一个
,则对于任意一个![]() 到
到![]() 的角
的角![]() ,可以把
,可以把![]() 表达成如下形式.
表达成如下形式.
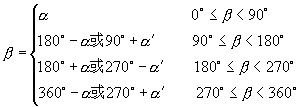
我们已经知道,![]()
![]() .
.
对于![]() 可用
可用![]()
![]() .
.
也可以![]()
![]()
对于![]() ,可用公式二,也可以利用
,可用公式二,也可以利用
![]()
![]()
对于![]() ,可用公五,也可利用
,可用公五,也可利用
![]()
![]()
![]()
![]()
![]()
![]()
一般地,![]() ,
,![]() 的三角函数值,等于
的三角函数值,等于![]() 的余名函数值,前面加上一个把
的余名函数值,前面加上一个把![]() 看成锐角时原函数值的符号.
看成锐角时原函数值的符号.
这样,任意角的三角函数值,都可以利用两套诱导公式去求.
(2)例题分析
【例1】求下列三角函数值:
(1)![]() ;(2)
;(2)![]()
解:(1)解法1:![]()
解法2:![]()
解法3:![]()
(2)解法1: ![]()
![]()
![]()
解法:2 ![]()
![]()
![]()
解法3: ![]()
![]()
![]()
说明:公式中的![]() 说是在
说是在![]() ~
~![]() 之间,事实上,这只是看法而已,
之间,事实上,这只是看法而已,![]() 可以是任意一个角,并不影响公式成立.
可以是任意一个角,并不影响公式成立.
【例2】化简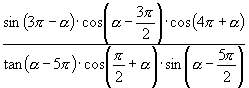
解:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
∴原式![]()
【例3】设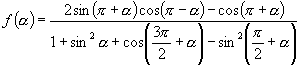 ,(
,(![]() ),求
),求![]() 的值.
的值.
解:∵![]()
![]()
![]()
![]()
![]()
∴![]()
![]()
![]()
![]()
![]() (∵
(∵![]() )
)
![]()
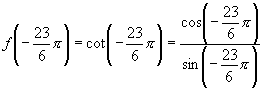
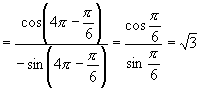
另解:![]()
![]()
【例4】求证: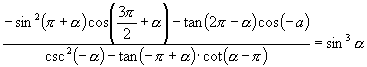 .
.
证明:∵![]()
![]()
![]()
![]()
![]()
![]()
![]()
∴左边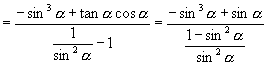
![]() 右边
右边
3.演练反馈(投影仪)
(1)求值
①已知![]() ,求
,求![]() 的值.
的值.
②若![]() ,且
,且![]() ,求
,求![]()
(2)化简:
①![]() ;
;
②![]() .
.
③![]()
参考答案:(1)
解:①∵![]()
![]()
![]()
![]()
解:②∵![]()
![]()
![]()
∴![]()
∵![]()
∴![]() 在第二象限
在第二象限
∴![]()
由![]() 可得
可得![]()
∴![]()
(2)解:①![]()
![]()
![]()
![]()
![]()
②![]()
![]()
![]()
(3)分类讨论
![]() 为偶数时,原式=0
为偶数时,原式=0
![]() 为奇数时,原式=0
为奇数时,原式=0
4.总结提炼
本节课我们在上一节课推导出来的五个诱导公式的基础上,又进一步学习了其他三个余名函数值的三组诱导公,两套诱导公式可以概括为![]() 的各三角函数值,当
的各三角函数值,当![]() 为偶数时,得
为偶数时,得![]() 的同名函数值;当
的同名函数值;当![]() 为奇数时,得
为奇数时,得![]() 的余名函数值;然后在前面加上一个把
的余名函数值;然后在前面加上一个把![]() 看成锐角时原函数值的符号,为了便于记忆,可以用口诀:“奇变偶不变,符号看象限”.灵活运用这两组诱导公式求任意角的三角函数值、化简或证明.
看成锐角时原函数值的符号,为了便于记忆,可以用口诀:“奇变偶不变,符号看象限”.灵活运用这两组诱导公式求任意角的三角函数值、化简或证明.
课时作业:
1.求下列三角函数值:
(1)![]() ;(2)
;(2)![]()
2.计算:![]() .
.
3.已知![]() ,求
,求![]() 的值.
的值.
4.化简:(1)![]() ;
;
(2)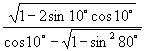 .
.
5.函数![]() 的值或是(
)
的值或是(
)
A.![]() B.
B.![]()
C.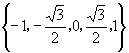 D.
D.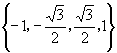
6.已知![]() ,求证
,求证![]()
参考答案:
1.解:(1)![]()
![]()
![]()
![]()
(2)![]()
![]()
![]()
![]()
2.解:原式![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3.解:由![]()
又![]()
![]()
![]()
4.(1)![]()
![]()
![]()
![]()
(2)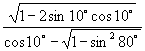
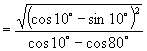
![]()
5.B,可以归纳:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…
,…
6.解:同![]() ,
,![]() ,
,![]()
∵![]()
![]()
![]()
![]()
∴![]()
说明:由诱导公式不难得出下列一组公式:
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()