第七节 相互独立事件同时发生的概率

教学建议

（一）教材分析

　　1．知识结构

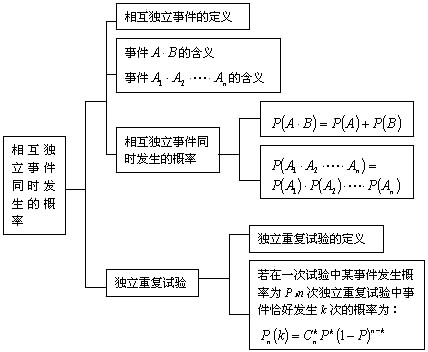
　　2．重点难点分析

　　重点是相互独立事件及其同时发生的概率和独立重复试验，难点是建立在n次独立重复试验中共事件恰好发生k次的概率计算公式．

　　（1）理解相互独立事件应当注意区别“互斥”与“相互独立”是两个不同的概念．前者指两个事件不可能同时发生，后者指一个事件的发生与否对另一个事件发生的概率没有影响．一般，两个事件不可能既互斥又相互独立，因为相互独立事件是以它们能够同时发生（如果其  中没有不可能事件）为前提的．要通过实例对比，加深理解．

　　（2）正确理解相互独立事件同时发生的概率

　　①两个相互独立事件同时发生的概率，等于每个事件发生的概率的积，即

．

　　②一般地，如果事件 相互独立，那么 个事件同时发生的概率，等于每个事件发生的概率之积，即 ．

　　注意：公式①适用的前提是 、 为互相独立事件；同样地，只有当 为相互独立事件时公式②才成立．

　　学习相互独立事件同时发生的概率乘法公式时，应注意相互独立事件的概率乘法公式只适用于相互独立事件，否则公式不能使用．如果所求事件是n个事件积的事件，用乘法公式求它的概率时，要突出强调这n个事件是相互独立的，否则公式同样不能使用．

　　（3）判断相互独立事件的关键

　　首先注意：“互斥”和“相互独立”是不同的两个概念：“互斥”指两个事件不能同时发生，而“相互独立”指一个事件是否发生不影响另一个事件的发生．显然两事件不可能既互斥（彼此发生有影响）又相互独立（彼此是否发生互不影响）．如果事件 与 是互相独立事件则： 与 ， 与 ， 与 ，也都是互相独立事件．

　　要注意，相互独立的几个事件，任一事件的发生，对其各个事件是否发生没有影响．但其中若干事件同时发生的事件可能对其余某一事件发生有影响．

　　（4）理解 次独立重复试验恰发生 次的概率公式

　　首先理解独立重复试验：指同样的条件下，重复地各次之间相互独立地进行的一种试验，也称为贝努力里试验．若在一次试验中某事件发生的概率是 ，那么在 次独立重复试验中这一个事件恰好发生 次的概率为 ．进行 次试验，试验的总结果中有些结果是 发生，其余是 发生，总结果是这样若干个 与若干个 的一种搭配．总结果中事件 恰好发生 次，则 发生 次，就是 个 与 个 的一种搭配．而符合条件的搭配种类又同， 和 出现的先后次序不同有关．在 次试验的总结果中，含 个 和 个 的搭配种类，相当于从 个号码中任取 个号码的不同取法的种数，共有 种，而所有这些搭配显然都是等可能的、且互斥，然后再根据相互独立事件的概率乘法公式，满足上述要求的每一种搭配发生的概率都是 ．

　　如果把 次独立重复试验中事件 恰好发生 次的概率记为 ，根据上述分析，可得为 ．

　　对上述公式要理解好，这对于灵活使用公式至关重要．

　　（5）二项分布与二项式定理的联系．

　　由于在 次独立重复试验中，事件 恰好发生 次的概率为： ．

　　如果令 ，利用二项展开式：

　　可见 就是 的展开式中的第 项，所以也把 叫二项分布公式，更进一步， 次独立重复试验中事件 至少发生 次概率为：

　　 ．设 则 且 ，正好是 的二项式展开式中的第 项且 ．

　　即： ， ．

　　有的书将公式 叫做二项概率公式．

（二）教法建议

　　1．建议从实例中引入相互独立事件的概念，以引起学生学习的兴趣．

　　2．教学中应强调一些容易混淆的概念之间的联系与区别，如弄清“相互独立事件”与“互斥事件”的区别与联系．

　　3．教师要强调运用各个公式的前提条件，防止学生在没有分清前提条件下就滥用公式．如应用独立事件同时发生的概率公式时，应注意两个前提：①事件之间相互独立；②这些事件同时发生．教学中还要注意对学生计算中出现的一些典型错误进行认真剖析．

　　4．在 次独立重复试验中，事件 恰好发生 次的概率 ，对这个公式应联系二项展开式的通项公式．

　　5．教学要在教学中向学生逐渐灌输解决有关概率问题的一般思路．一般来讲，要先判断问题中有哪些简单事件，并用字母（如 等）表示出来，再用 或 、 、 的函数式于将所求事件表达出来，这其中往往要用到些运算律，如 等．最后，恰当地选取概率的加法或乘法公式，求出所求事件的概率．

返回页首