第十节 球

教学建议

（一）教材分析

1．知识结构

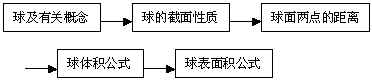
2．重点难点分析

　　本节教学的重点是球的概念和性质以及球面表面积和球体体积公式．教学难点为球面上两点的球面距离及相关问题，球的体积公式推导方法的理解及有关球的接、切问题的解决．

　　（1）球是教材中唯一的旋转体．在此之前学生对曲面是比较陌生的，所以在引入球的概念时，先需重点介绍曲线段旋转形成曲面的过程．通过球面了解曲面的特性，通过作球的截面进一步认识球与圆之间的关系．而球的体积和表面积公式的推导方法又是首次使用，又是在以后学习中有重要价值的方法，但由于学生没有学过极限，不容易真正接受这种化整为零，再积零为整的极限思想，总觉得差一点，不是绝对相等，所以在教学中要特别提醒学生用这种方法计算出的体积和面积都是精确值而不是近似值．

　　（2）球与多面体组成的组合体问题，这种两个几何体的关系关键是把握基本元素间的关系，这要求学生能发挥空间想象能力，分析图形特征，否则无法找到合适的截面，即使画出截面也无法准确翻译立体图与平面图各量间的关系，为此这个难点需要新旧知识的结合，需要教师在教学中帮学生总结归纳作截面的方法．

（二）教法建议

　　（1）球的概念在引入时，应让学生明确球面与球体的区别，可借助教学软件演示半圆旋转过程及球面生成过程，还可借助生活中熟悉的足球，篮球乒乓球等实物帮助理解球体的含义．还可以从学生熟悉的圆开始，把平面图形发展到空间，故球面还可以定义为到定点的距离等于定长的点的集合，从而一开始就把球与圆结合起来，找出二者的联系，便于研究球的截面．

　　（2）关于经度和纬度，学生在学习地理时已经了解且熟悉，而数学中的经度和纬度则是二类重要的角—面面角和线面角．因此这正是将前面所学的线面关系运用于多面体与旋转体的最佳时机，教师可根据概念的要求让学生分别做出合乎题意的线面角和二面角的平面角，这样在构造的过程中将球的半径，小圆半径和纬度之间的关系搞清，同时为球面距离的计算做好准备．

　　（3）球与其它多面体之间的接切问题，在课本中没有明确的定义，在教学中应首先与学生统一接切的认识，再通过简单的正方体或正四面体与球的接切，让学生看清截面的作法，了解两个几何体基本元素之间的关系，特别要强调截面在构造上的要求，并总结截面的作法．