第十节 解斜三角形应用举例

教学建议

知识结构

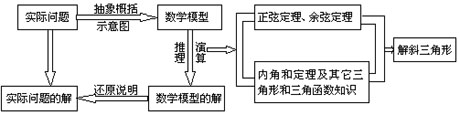
重点难点分析

　　本节重点利用解斜三角形解决相关实际问题．解斜三角形知识在生产实践中有着广泛的应用，解斜三角形有关的实际问题过程，贯穿了数学建模的思想．这种思想就是从实际出发，经过抽象概括，把它转化为具体问题中的数学建模，然后通过推理演算，得出数学模型的解，再还原成实际问题的解．强化上述思维过程，既是本节的重点，又是本节难点．

　　解三角形应用题的另一个难点是运算问题，由于将正弦定理、余弦定理看成几个“方程“，那么解三角形的应用题实质上就是把已知信息按方程的思想进行处理，解题时应根据已知和未知合理选择一个“容易解”的方程，从而是解题过程简洁．同时，由于具体问题中给出的数据通常是近似值，故运算过程一般较为复杂，必须借助于计算器计算，因此要加强训练，达到“算法简炼，算式工整，计算准确”的要求．

教法建议

　　1．复习提问正弦定理、余弦定理以及分别用它们解斜三角形的基本情况，而后指明，实际问题形式多样，简单结论不能概括，提出新的例题引入新课．

　　2．在教学中，要引导学生重视分析题意，理解问题的实际背景，如何将实际问题中的各种要素提出来，分清已知与所求，根据题意画出示意图，确定所需的数学知识，从而建立数学模型．根据数学模型启发学生正确运用正弦定理和余弦定理，在演算过程中，力求算法简练，算式工整，计算正确，并且自己作出示范，严格要求学生．

　　3．讲解例题时不妨让学生讨论归纳出应用题一般思路，数学模型的建立，从而能使学生更好的掌握．

　　4．如果有条件，最好采用多媒体演示例题中模型，帮助学理解问题的背景，建立模型，同时要求学生要注意观察周围生活的事物．

返回页首