第九节 函数y=Asin(ωχ＋φ)的图象

教学建议

知识结构：

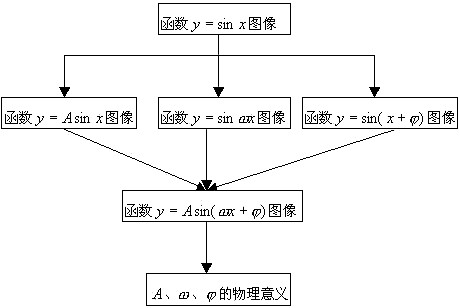
重点与难点分析：

　　本节重点是用“五点法”画函数 的简图，以及由函数 的图像得到函数 图像的变换过程．“五点法”作图在对图像要求不精确时经常用到，是数形结合中画图常用的方法．图像变换体现了数学的由简单到复杂的转化，由特殊到一般的化归思想，要掌握三角函数的图像变换，关键理解A、 、 对图像变换所起的作用．

　　本节难点是当 时，函数 ， 的图像间的关系．学生在这里经常出错，教学中要帮学生尽量克服这一难点．首先要学生理解A、 、 三个参数的名称、在变换过程中的作用，函数 的图像如何通过 逐步变换得到的，A、 、 三个参数对于图像有什么样的影响．变换的顺序不同 、 变换的数据可能就不相同，让学生理解所的变换均是针对x而言的，关键是看x是如何变化的．

教法建议：

　　1．本节的主要内容是“五点法”画函数 的图像，以及由函数 图像到函数 的图像的变换过程．首先让学生理解由函数 的图像分别到函数 ， ， 图像，是如何变换得到的以及参数 、 、 分别对变换图像影响．讲解过程中一定要结合图像，让学生掌握变换的思路．讲解后配上适当的练习进一步熟悉变换过程．每个例题讲解图象变换的目的，在于揭示各种正弦函数图象的内在联系，而并不要求用图象变换来作图，而是为 图像的变换奠定基础．

　　2．由函数 图像变换到函数 的图像过程中，变换的顺序不同可能变换的量不相同，例如先变相位，再变周期，与先变周期．再变相位，相位变换的量不同，函数 的图像可由函数 的图像上所有点向左平_，再将所得各点的横坐标缩短到原来的 ；也可先将函数 的图像上各点的横坐标缩短到原来的 ，再将所得各点向左平移．这一不同学生很难理解，学生很容易出错，也是经常考查内容．首先给学生说明对于 中的 、 均是针对x而言的，因此在变换的过程关键就看x变换了多少，其它因素暂时不考虑．可以借助多媒体课件讲解，能起到更好的效果． 

　　3．画函数 的简图，主要还是先找出确定曲线形状时起关键作用的五个点．要强调一下：这五个点应该是使函数取得最大值、最小值以及曲线与 轴相交的点；找出它们的方法是换元法，设 ，由X取0， ， ， ， 来确定对应 的值．在每道例题中讲图象变化的目的，在于揭示函数 的图象与正弦曲线的关系，而不是要求按图象变化规律来画图，这样可以借助函数 的性质研究函数 的性质．

　　4．由于函数 的图象在物理和工程技术的很多问题中应用都很多，所以，在引入函数 的图象时，就可以从物理中的一些实际问题出发，即结合了实际，又体现了学以致用的思想，特别是对 、 、 物理意义的理解。比如可以举物体作简谐振动时位移s与时间t的关系。     

返回页首