第七节 二倍角的正弦、余弦、正切

教学建议

　　1．倍角公式可以由学生根据和角公式直接推导出，在对 公式的推导中让学生完善角的范围限制．公式推出后，让学生将倍角和前面所学的和（差）角公式的联系图总结出来，使知识系统化．

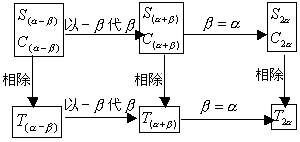
　　2．由学生讨论分析公式的特点．①公式中的角之间存在2倍关系，其中要强调倍角的相对性，打破学生习惯认为只有 ， 才具有2倍角关系，教学中通过一些简单实例加强这方面的训练，熟悉公式的正向、逆向运用，如 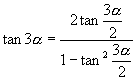， ， ， ， 等．②利用 求 只需要已知 即可，利用 求 时需要已知 ，观察 左侧的特点，可以与 建立联系，能否将公式变形？引导学生推导出 的两个变形公式，因此已知 中之一即可求出 ．③由单角变为倍角时式子的幂降升高，相反由倍角变为单角时式子的幂降低，在求解、化简或证明时要注意分析角之间、式子幂之间的关系，整理将形式统一．
　　3．讲解例1时给学生指出或让学生归纳出：已知角 的某个三角函数值及其角所在的象限不仅可以求出 其余的三角函数值，还可求倍角的三角函数值．
　　4．课本在例2的分析中给出将结论变形求解的方法，学生感觉方法巧妙的同时，还困惑理解方法如何想到的，给学生分析：证明三角等式一般要观察分析等式两边的联系区别，主要从角和函数名称入手，尽量将角和函数名称统一，此题左右两侧的角形式和函数名称都相同，分子中的角都是 4倍的、函数名称都是正弦、余弦，分母上都是单角而且函数名是正切，直接从左或右向另一侧证明有些困难，能否将结论适当的变形以便于求解？使学生了解整个题目分析的过程．
　　5．解决本章开始所提的问题，是倍角公式的实际应用，利用三角函数线学生可以得到 ，得到本题的结论．另外还需要把题目中“半圆”的条件替换为“圆”，可以的得到正方形的性质：在一个圆的所有内接矩形中，内接正方形的面积为最大．
　　6．例4、5是利用和（差）角、倍角公式推导出了半角公式、和差化积以及积化和差，这些公式不要求记忆，但要求学生在给出公式时会利用这些公式，掌握公式的推导过程．