 设为首页
设为首页
 加入收藏
加入收藏
教学建议
一、重点、难点分析
本节教学的重点是能够画出已知线段的和、差、倍、分.教学难点是相关概念的理解以及画法的掌握.
1.线段和线段的长度
“线段”是一个几何图形,它具有其形状、位置和大小,对于两条线段来说,它们的形状相同,都是直线的一部分,但它们可能处在不同的位置,其大小也不一定相同,如长方形的相邻的两条边,它们都是线段,但所处的位置不同,且大小也不同;而正方形的相邻两边,它们虽处的位置不同,但大小是相同的,一条线段的大小,可以用它的“长度”来刻划,“线段的长度”是用长度单位度量而得到的,它是一个带着长度单位的正数,由此可见,“线段”和“线段的长度”是两个完全不同的概念,前者是一个图形,后者是一个数量.
2.线段的比较
比较两个小朋友的高矮,可以让他们站在一块平地上,让他们的脚底平齐,再看他们的头项.
比较两条线段时,也可用类似的方法,通过图形来比较,即将它们移至同一条直线上,使它们的一对端点重合,另一对端点落在重合端点的同侧,通过对这两个端点的位置的观察比较出这两条线段的大小.
![]()
![]()
![]()
(1) (2) (3)
比较两条线段AB,CD的长短,首先将它们移到同一条直线上,使一个端点A和C重合,另一个端点B和D落在直线A和C的同侧,如果点D和B重合(图1)就说线段AB和CD相等,记作AB=CD.如果点D在线段AB上(图2)就说线段AB大于线段CD记作AB>CD,如果点D在线段AB外(图3),就说线段AB小于CD记作AB<CD.比较两条线段的大小也可分别度量出它们的长度通过对数量的大小的比较来说明线段的大小,“两条线段相等”是说明这两条线段“长度相等”.
![]()
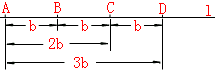
3.线段的中点
在图中,点B把线段AC分成两条相等的线段,点B叫做线段AC的中点.这时有,AC=2AB=2BC,AB=BC=![]() AC.从图中,我们还可以看到点B和点C把线段AD分成三条相等的线段,点B和点C叫做线段AD的三等分点.
AC.从图中,我们还可以看到点B和点C把线段AD分成三条相等的线段,点B和点C叫做线段AD的三等分点.
4.线段公理
所有联接两点的线中,线段最短.这个公理也可简述成:两点之间、线段最短.连结两点的线段的长度,叫做这两点的距离.这个公理在实际中的应用是很广泛的.例如为了节省材料,降低造价,从A地到B地架设电线,总是尽可能沿着线段AB架设.
二、知识结构
![]()
三、教法建议
1.线段的比较习惯上是说比较长短,但是为了和其他量的比较相一致,也把它叫做比较大小.比较的结果也用符号等于“=”、大于“>”、小于“<”来表示.要让学生熟悉这里的语句表示和符号书写.
2.联系小学学过的用刻度尺度量线段的长度,说明线段的度量实际上就是看这条线段与刻度尺上哪一条线段相等.因此,线段的比较也可以通过度量来进行.就是说,长度大的线段较大,反过来,较大的线段它的长度也较大.教学时要注意使学生对图形的认识与对数量的认识结合起来.以图形的认识为主,首先从图形上说明线段的比较,这是几何的本身特点,然后再与数量紧密联系起来,比较线段的长度,这两者是一致的,达到数与形的结合.
3.关于线段的比较、两条线段的和差、一条线段的几倍与几分之一,是先以图形直观给出,再说明它们与线段的有关度量的一致性.以图形的认识为主,这是几何研究问题的主要特点,同时联系到数量,使两者一致起来,达到形和数的结合.教学时要注意通过这部分内容培养学生的识图能力.关于线段的画法,也是给出了用圆规截取和用度量的两种方法.要使学生能够画出正确的图形,暂不要求写出画法.
4.关于直线的公理——经过两点有且只有一条直线,是经过演示、实践后以公理的形式出现的.关于线段的公理——两点间线段最短,也是经过演示、实践后给出的.要在学生真正了解并确信这些公理的前提下记忆这些公理.提出公理之后还介绍了它们的一些实际应用,使学生进一步了解这些公理的意义.
四、线段中点的三种表示方法
在线段上,把一条线段分成两条相等的线段的点叫线段的中点.如图,C是线段AB的中点,则可以表示为:(1)![]() ;(2)
;(2)![]() 或(
或(![]() );(3)
);(3)![]() (或
(或![]() ).
).
![]()
五、线段的和的画法
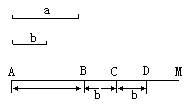
举例:已知线段a、b(a>b)用圆规和直尺画出线段m,使m=a+2b
画法:1.画射线AM
2.在射线AM上截取AB=a
3.在射线BM上顺次截取BC=CD=b,则线段AD=a+2b,即为所要画的线段m,如图所示.