第一节 直线

教学建议

　　一、重点、难点分析

　　本节教学的重点是直线的表示方法，直线的公理及相交线．本节教学的难点是两直线相交为什么只有一个交点的理解，直线公理的理解．直线是中学几何教学中所研究的第一个点集，掌握直线的定义、表示方法、以及直线公理等相关知识点是进一步学习射线、线段以及直线与直线的位置关系等相关知识的基础．

　　1． 直线

　　一根拉得很紧的线给我们以直线的形象，直线是向两方无限延伸的．在代数中，数轴就是一条直线，它是规定了原点、正方向和单位长度的直线，数轴是可以向两个方向无限延伸的．

　　我们可用直尺画直线，如图(1)就是一条直线．

　　2． 直线的表示方法
几何中我们常用字母来表示图形，一个点可以用一个大写字母来表示，如图(2)中两点分别用字母A和B表示，这两点分别记作点A和点B．

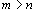
　　一条直线可以用在这直线上的两个点来表示，如图(2)中的直线可以记作直线AB．一条直线也可以用小写字母表示，如图(2)中的直线可以记作直线l．

　　3． 点与直线的位置关系

　　一个点在一条直线上，也可以说这条直线经过这个点，如图(9)中点P在直线l上，也可以说直线l经过P点．一个点在一条直线外，也可以说这条直线不经过这个点，如图(9)中点A在直线l外，也可以说直线l不经过A点．

　　　4． 关于直线的公理

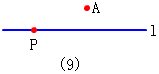
　　 用一个钉子把一根木条钉在墙上，木条可以绕着钉子转动，如图(3)．

当用两个钉子把一根木条钉在墙上，木条就被固定了，如图(4)．

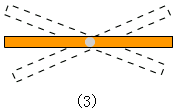
　　事实表明：经过一点有无数条直线，如图(5)．

　　经过两点有一条直线，而且只有一条直线，如图(6)．

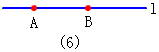
　　关于直线的公理：经过两点有一条直线，而且只有一条直线．也可以简单说成：过两点有且只有一条直线．

　　关于直线公理的应用，日常生活中常用到此公理，如：建筑工人砌墙时，经常在两个墙脚的位置分别插一根木桩，在两根木桩之间拉一条绳子，定出一条直的参照线，又如植树时，只要定出两个树坑的位置，就能确定同一行的树坑所在直线．

　　5． 相交直线

　　当两条不同的直线有一个公共点时，我们就称这两条直线相交或称它们是相交直线，这个公共点就是它们的交点，如图(7)．

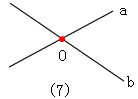
　　直线a和b相交，点O是它们的交点．

　　二、知识结构

　　本小节描述了关于直线的意义，说明了直线的表示方法、点和直线的位置关系、关于直线的公理以及关于两条直线相交的意义．

　　三、教法建议

　　1、本节内容对以后的几何学学习有打好基础的作用．

　　2、教师要注意引导学生在具有充分感性认识的基础上了解直线的意义以及点和直线的位置关系．

　　3、引导学生在了解并确信直线公理的前提下记忆这些公理，并了解他们的实际应用，进而理解公理的意义．

　　4、帮助学生认识到几何研究问题的主要特点——以图形认识为主，同时联系数量，达到数形结合．

　　5、教学过程中注意渗透思想教育．

返回页首

教学建议

　　一、知识结构

　　二、重点、难点分析

　　角的定义既是本节教学的重点，也是难点．本节知识建立在射线、线段等相关知识的基础上，同时也是进一步学习角的度量、比较、画法，以及深入研究平面几何图形的基础．

　　1．角的定义是由实际生活中具有角的形象的物体抽象出来的，理解角的定义一定要明确角的边为射线，角为平面内的点集．角也可认为是一条射线绕它的端点从一个位置旋转到另一个位置而形成的图形，这里的线动成角体现了运动变化的思想．

　　2．角的表示法，小学没有介绍，这里首先说明用三个字母记角．对此，要特别强调表示顶点的字母一定要写在中间，唯有在顶点处只有一个角的情况，才可只用顶点一个字母来记这个角，否则分不清这个字母究竟表示哪一个角．在讲往数字或希腊字母来记角时，可再让学生作些练习，说出所记的角怎样用三个字母来表示． 

　　三、教法建议

　　1．本节教学可以在简单复习直线、射线、线段的基础上引入，将问题的研究方向转向这些最基本的几何图形与点结合以及互相结合能够组成什么图形．可以尝试让同学们摆火柴，重点应在具有角的形象的图形，然后可以在列举、观察、分析学习、生活、生产中同样具有角的形象的物体的基础上，让同学们尝试给出角的定义．

　　2．关于角的另一种定义，也可以通过实物演示的方式得出，冽如一手扯住线的一端，另一手拉住线的另一端旋转．重点应是对运动变化的观点的渗透．平角和周角也可以让学生给出，真正理解“平”与“直”的含义．

　　3．教学过程中可以给出一些判别给定图形是不是角的练习，帮助学生理解角的相关概念．同时将角的知识与学生的生活实践紧密的结合起来．可以充分发挥多媒体教学的优势，结合图片、动画、课件辅助教学．

返回页首